COSMOLOGY OF A BINARY UNIVERSE

Part 1:

The Origin, Properties and Thermodynamic Evolution of a Universal Wave and Force Field

Contents of Part 1

1. Introduction

2. The current cosmology of general relativity

3. Properties of a Universal Wave and Force Field (UF)

3.1. Dynamics and Thermodynamics

3.2. Longitudinal and transverse waves

3.3. Gravitational force

4. Cosmological origin, nature and thermodynamic evolution of the UF during an interrupted Carnot Cycle

4.1. Initial postulate of the existence of a cosmic fluid

4.2. Cavitation or rupture of the cosmic fluid

4.3. Isothermal expansion of vapor filled cavity to critical size

4.4. Adiabatic collapse and compression of the cosmic vapour to form baryonic matter

4.5. The Big Bang

4.6. Adiabatic expansion through cosmic time after the Big Bang during an interrupted Carnot Cycle

4.7. Critical conjunction point C*

4.8. Current accelerated isothermal expansion

4.9. Summary of Part 1

References

Appendix A: Thermodynamic Properties of an Isothermal Gas Law for the Chaplygin/Tangent Field

Appendix B: A New Explanation for the Anomalously Weak Tensile Strengths of Liquids and Solids

Appendix C: Physical Derivation of the Schrödinger Equation of Quantum Mechanics from the Concept of a Universal Wave Field

Appendix D: Philosophical Caveat

[Part II : The Origin of Matter, ‘Dark’ Matter and ‘Dark Energy’ is in preparation].

Note In this monograph, in all pressure- volume equations unit mass is assumed, so that v and ρ then refer to specific volume and specific density. Also, mass in our present system is taken to be dimensionless; this convention simplifies the notation, and is physically supported in the theory, since it is agreement with our definition of mass as a ratio of energies i.e. m_b / m_q = [n+1]^1/2 where m_q is a quark mass, m_b is any baryon mass and n is a pure number representing the partition of the energy of the system. This will be discussed in Part II: Origin of Ordinary Matter ( under preparation).

1.(I) Introduction

Current cosmologies have from the Newtonian dynamical cosmology of classical physics which dealt with mass particles and forces, and then from general relativity which introduced its field theory of gravitational force based on mass-induced distortions in the geometry of a postulated but non-observable space-time continuum. This general model had been adjusted periodically with advances in quantum mechanics and particle physics to become the Standard Big Bang Cosmology with considerable success.

The basic physical facts about the universe on our present knowledge are that it is about 13.7 billion years old, spatially flat, and not only expanding but doing so at an unexplained accelerated rate. It is roughly made up of ordinary matter (4%) exotic dark matter (20%) and dark energy 76%.

However, in the current theory there are many limitations. Specifically, we do not know the origin of ordinary matter. We do not know the nature or origin of either the dark matter, or the so-called dark energy. We do not know how to integrate gravitation and general relativity with quantum theory. We do not know how radiation physically travels in space nor how gravitational force is transmitted through space. We do not know how the Big Bang’s enormous energy and temperature came about. We currently do not know for certain how inflation came about nor even if it is real. We do not know why the cosmos is accelerating in its expansion. General relativity is apparently powerless to answer these questions so that there is a need for some more comprehensive and basic explanation [1].

Here in Part I we shall present the physical theory of a Universal Wave and Force field (UF), related to the Chaplygin/Tangent gas of aeronautics and astrophysics, which offers new answers to most of the above questions. We then present a cosmological Carnot cycle for this UF, starting in the pre-Big Bang era, continuing with explanations for the emergence of ordinary matter and radiation after the Big Bang and leading up to the evolutionary cosmic expansion of the cosmos since then.

In Part II, currently under preparation, we shall deal with the origin of matter in more detail and explore the emergence of the dark matter and dark energy of the universe.

2 (I). General Relativity Cosmology

The present standard cosmology is based on the theory of general relativity, and so we first must briefly examine its formulation, assumptions and limitations before presenting our new cosmology. The current theory models a unitary universe made up of galaxies and interstellar gas clouds as an incompressible, hydrodynamic assemblage having pressure p and density ρ within a geometrical space-time continuum in which the masses and mass particles generate the distortions of the metric from which gravitational force emerges.

The Friedmann formulation of general relativity [2,3] is as follows:

(2/R) (d²R/dt²) + (1/R²) (dR/dt)² = 8πG p/c² − k/R²

(dR/dt)² = (8π/3) GρR² −k

where R is the radius of the cosmos at any time t, G is the universal gravitational constant, and k is a constant related to the metric which describes the geometry of the space- time continuum.

If we introduce the Hubble relationship V = HR, (where V is velocity of expansion) we get an alternative Friedmann formulation

H² 8π/3 Gρ = − k/R².

The Friedmann equation is readily compared to the various Newtonian dynamical formulations [3]. For example, if p = 0 we get the Newtonian model

2/R(d²R/dt²) = GM_o/–kR = 4/3 π GρR² −k.

In this classical model, if k is 0 or negative then the radius of the cosmos R increases indefinitely. If k is positive, then R increases to some maximum size R_max. Also, we are restricted here to the cases where V <<< c and p <<< ρc². In general relativity, such as with the Friedmann formulation, there is no such restriction.

From the Friedmann model other general relativity formulations, such as those of Einstein, Eddington-Lemaitre, de Sitter, Einstein-de Sitter etc., are readily derived [2,3].

The assumptions of the general relativity cosmology are (1) the universe is homogeneous and isotropic,(2) there exists a universal geometric construct called the space-time continuum, which has the physical property of sustaining stress. In the limit of finite, uniform, relative velocities the laws of special relativity apply, while in the limit of very small velocities the equations reduce to those for Newtonian motion.

A basic postulate derived from the special theory also applies, namely that uniform motion (i.e. force-free motion) through space cannot be detected experimentally (the speed of light being the same for all inertial observers). The experiments that are used to attempt to detect motion through space involve various types of optical instrumentation such as interferometers and oscillators, and the special relativity proposition is equivalent to saying that light does not travel through space in any physically real medium.

Such a proposition is today confronted with the generally small but universal physical effects of both uniform and accelerated motion that are readily detectible with modern optical and resonant instrumentation.( www.energycompressibility.info) However, the experimental confirmation of various physical effects of motion through space are met either by dismissing them as being statistically insignificant, or by making successive adjustments to the Einstein cosmological constant, which is an arbitrary energy term added to his field equations to account for such things as dark energy and acceleration in the rate of cosmic expansion.

General relativity offers no explanation for the existence of matter, nor for the quantum nature of gravity. It has no explanation for the Big Bang singularity, nor does it extend before the instant of that event. Its explanation for the transmission of gravitational attraction through space is based on the assumption of the existence of the space-time continuum construct which allows no direct experimental verification of its reality.

To repeat, its basic tenets are its assumptions of general invariance and the impossibility of detecting any absolute uniform motion through space; i.e. there is assumed to be no universal underlying physically real medium, only its postulated, geometrical, space- time continuum.

Another important technical limitation of general relativity and its cosmology is that it is a differential field theory, and so solutions to its differential equations of motion require a knowledge of the appropriate boundary conditions. In the case of local applications, the boundary conditions can often be specified or assumed so that solutions can be obtained. In the case of cosmology, however, the boundary conditions are those of the entire cosmos and are essentially unknown – indeed, perhaps unknowable. This is a fundamental limitation of all differential field theories when applied to the entire cosmos. Another drawback with differential field theories is that they have difficulties in dealing with singularities. Physical singularities such phase changes and the Big Bang tend to become infinities in the differential field theories. We now describe the physical basis for a new alternative cosmology which, being based on an integral equation of state, avoids this problem..

3.0 (I). PHYSICAL PROPERTIES OF A UNIVERSAL WAVE AND FORCE FIELD (UF)

3.1 (I). Dynamics and thermodynamics of the Chaplygin/Tangent gas

To describe the motions of any compressible fluid continuum, three basic equations are needed:

1.Euler’s classical hydrodynamic equation of motion:

For 1-dimensional flow this equation is

∂u/∂t + u ∂u/∂x + v ∂u/∂y +w ∂u/∂z = −(1/ρ) ∂p/∂x

where the term on the right hand side is called the pressure gradient force.

2. The equation of continuity, or conservation of mass:

∂ρ/∂t + div (ρw) = 0.

3. Equation of State: relating pressure p to specific density ρ ( or to its reciprocal, the specific volume v = 1/ρ)

(a) For real physical gases undergoing adiabatic motions ( i.e. no heat flow, dQ = 0) the general equation of state is :

pv^k = constant.

The wave speed c is given by c² = kpv. Here k, the ratio of the specific heats (k = c_p/c_v ), is the adiabatic exponent (sometimes also denoted by γ). The adiabatic exponent ratio k is related to n the partition parameter- roughly equivalent to the number of ways the energy of the system is divided- by k = (n+2)/n; n = 2/(k−1).

(b) For isothermal motions in a real gas ( i.e. no temperature change, dT = 0) the equation of state becomes

pv = RT or p/ρ = RT.

Real gas equations of state all lie in Quadrant I of the pressure –volume field of Figure 1 below.

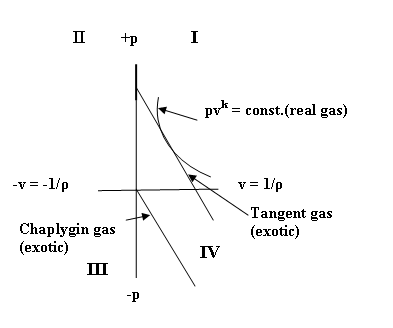
Figure 1. Pressure-volume relationships in compressible fluids

Quadrant 1: Real gases and Tangent gas (exotic)

Quadrant IV: Chaplygin gas and Tangent gas (exotic gases)

3.1.1. Adiabatic Equations of State for Compressible Fluids where k= −1: The Chaplygin/Tangent gas

For real gases and fluids the adiabatic exponent k = c_p/c_v is always positive in the adiabatic equations of state. However, if k is, instead, taken as being a negative number then the properties of the resulting theoretical fluid change radically. In 1901 a Russian aerodynamicist, S. Chaplygin, first proposed [4] this purely theoretical, compressible fluid, now called the Chaplygin gas having k = −1, to help calculate certain features of jet flow in gases. Since his theoretical gas did not apparently exist in our known physical world, it has had little application, except for simplifying some calculations in aerodynamics [5].

Within the last five years, however, the cosmological problem raised by an unexplained acceleration in the expansion of the universe has been cited by some cosmologists [6,7,8] as indicating that a fluid called the Chaplygin gas may exist physically as an exotic universal “cosmic fluid” which is the seat of the so-called ‘dark energy’ of the universe, presently calculated to comprise about 76% of the total ‘matter’ of the cosmos.

The Chaplygin gas has the adiabatic equation of state

pv^-1= p/v = p ρ = constant, or

p = −Av = −A/ρ

where p is the pressure, v = 1 /ρ is the specific volume, ρ is the density per unit mass of fluid and A is a positive constant. This equation plots with negative slope dp/dv on the pressure-volume diagram ( Fig. 1 above) and its pressure p is always negative. This possibility of a negative pressure is the attractive feature for the present day cosmologists who are concerned with the apparent accelerated expansion of the universe, and the Chaplygin gas is increasingly being proposed as a physically real exotic cosmic fluid to address this cosmological problem. Its properties are quite bizarre compared to our real world gases. The Chaplygin gas lies entirely in Quadrant IV of Figure 1.

While the success of the Chaplygin gas in rescuing general gravitation and superstring theories of gravity from their current difficulties is problematical, it also has properties pointing to a much broader universal wave and force field existing in Quadrant I, and it is this we investigate here.

A closely related fluid to the Chaplygin gas is called the Tangent Gas [5] which has an equation of state identical to the Chaplygin gas except for the addition of a constant B. It may lie in either Quadrant 1 or Quadrant IV of Figure 1. Its equation of state is

pv^-1 = constant, or

p = −Av + B = −A/ ρ +B.

In this form the pressure p is positive for values of Av less than B. The relationship became very useful to aerodynamics in the 1940’s. As a tangent curve to the adiabatics and isotherms for ordinary atmospheric air, the “tangent gas” provided a linear relationship between pressure and density, which, for small variations of these variables, gives a useful approximation to the more cumbersome, exact, non-linear thermodynamic equations. It was only very recently during the present examination of the Chaplygin gas that the special properties of the tangent gas as a fundamental cosmological fluid became apparent.

Figure 1. Pressure-volume relationships in compressible fluids

Quadrant 1: Real gases and Tangent gas (exotic)

Quadrant IV. :Chaplygin gas and Tangent gas (exotic gases)

3.1.2. A New Isothermal Equation of State for the Chaplygin/Tangent gas

Recently [21] a new isothermal equation of state has been derived for this peculiar fluid field, as follows:

The generalized adiabatic equation of state for the fluid with k = −1 is pv^k =constant, and so this becomes

p v^-1 = p/v = const. = ± A, or

p = ± Av

We now must choose the sign before the positive numerical constant A, and this will determine the slope of the equation of state in the p-v field. In the case of the Chaplygin gas the sign is chosen as negative so as to give p = −Av = −A/ρ, and for the Tangent gas as p = −Av + B = −A/ ρ +B , mainly because this makes them both agree with all real gases in having negative slope − dp/dv on the p-v diagram and also guaranteeing a positive wave speed with c² = +dp/dρ.

However, there is also no apparent reason to completely reject the alternative choice of +A for the equation of state, that is, to chose a positive slope for dp/dv. This would give the isothermal equation of state for the fluid:

p =+ Av through the origin and

p = +A/ρ –B in Quadrant I.

These two new isothermal curves with positive constant A are strictly orthogonal to the adiabatic Chaplygin and Tangent gas curves. They constitute an isothermal equation of state for the fluid with k = −1, since p/v =+A, and, if the positive constant A is set equal to a constant temperature + A =RT ,we would then have p/v = RT= constant which is certainly an isothermal relationship.

We then have :

Real gases ( k ≥ 1) : pv>¹ = constant = +A is the general adiabatic equation of state

Real gas ( k = 1) : pv⁺¹ = constant. = +A = RT is the isothermal gas or the equation of state for any ideal gas with constant temperature T

Exotic gases ( k = − 1) :

a) Chaplygin gas: Adiabatic equation of state p = −Av = −A/ρ

Isothermal equation of state p = Av = vRT; p/v = RT

b) Tangent Gas Adiabatic p = −Av + B

Isothermal p = +Av − B

We now propose to treat these exotic states, not as separate physical entities or ‘gases’ but instead as simply the adiabatic and isothermal equations of state of one single, universal compressible field ( UF).

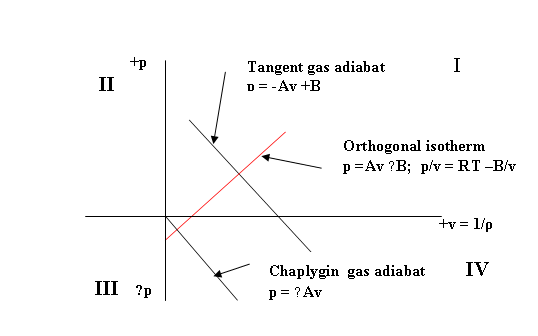
Figure 2. Equations of State for the Universal Field (k = − 1; pv^-1 = const.)

For a more complete report on the theoretical derivation of the isothermal gas see Appendix A: Thermodynamic Properties of an Isothermal Gas Law for the Chaplygin/Tangent Field

3.1.3. The Energy Equation

An additional useful relation for any compressible field is the energy flow equation relating compressive wave speed c to relative flow velocity V:

c² = c_o² – V²/n

where n ( =2/k – 1) is the number of ways the energy of the system is partitioned. If we divide through by the square of the static wave speed c_o² we get the wave speed ratio

c/c_o = [ 1 – V² / n c_o² ]^1/2

which ( when n = 1 ) is formally identical to the Lorentz/Fitzgerald contraction factor of special relativity theory.

For unsteady or pulsed flow, the energy equation becomes c² = c_o² – V²/n – 2cV/n where the additional, or ‘pulse’ term, 2cV/n is of great importance in quantum phenomena.

3.2. (I) A Universal Wave and Force Field: Longitudinal and Transverse waves

As stated, the evidence seems to be that, instead of there being three separate exotic “gases”( Chaplygin gas, Tangent gas and Orthogonal or isothermal gas), there is only a single, compressible, fluid entity or field, namely a universal field (UF) having the usual adiabatic and isothermal equations of state.

We now explore the proposition that there exists this single Universal Field (UF) having compressible properties of the adiabatic Chaplygin/Tangent gas, and the new isothermal orthogonal gas, which supports stable waves uniquely obeying the classical wave equation for both transverse and longitudinal vibrations. It will then be shown that its transverse waves correspond to Maxwell’s electromagnetic waves of light, while the longitudinal vibrations correspond to waves which transmit gravitational force through space.

3.2.1. Equations of State relating pressure , p, to specific density ρ ( = 1/v) and where n =−1; k = (n+2)/n = −1:

Adiabatic: p = −Av + B = −A/ρ +B (/Tangent Chaplygin gas)

Isothermal: p= +Av −B ; p/v = RT (Orthogonal Gas)

3.2.2. Energy Equation : ( relating wave energy c² to kinetic or flow energy V², and wave speed c to relative motion V)

c² = c_o² – (1/n) V²

and, with n = −1 we have

c² = c_o² + V².

If we divide through by the static wave speed c_o² we get

c/c_o = [ 1 – V² / n c_o² ]^1/2

and with n = − 1 we now have

c/c_o = [ 1 + V² /c_o² ]^1/2.

3.2.3. Force in the Universal Field (UF)

In the UF the force is given by the Euler equation which, for 1-dimensional flow, is

∂u/∂t + u ∂u/∂x + v ∂u/∂y +w ∂u/∂z = −(1/ρ) ∂p/∂x.

3.2.4. Longitudinal Wave Motion in the UF

The Universal Field is unique in that (1) it is the only field in which the Classical Wave Equation is strictly valid and which therefore can transmit stable longitudinal waves, of either condensation or rarefaction, of any amplitude, and (2), as we shall see in Section 3.2.9 below, it is the only tenuous fluid which can support and transmit transverse waves.

In general, the adiabatic speed of sound waves c in a fluid is related to the pressure p and density ρ by the equation

c² = (dp/dρ)_s.

From this, the adiabatic ( i.e. no heat flow, ∆Q = 0) speed of sound c in a perfect gas is also given by

c² = kpv = kp/ρ =kRT.

A positive wave speed c, therefore requires that dp/dρ must be positive. Since v = 1/ ρ, we see that dp/dρ and dp/dv must have opposite signs. Real gases, and the adiabatic equation of state for the UF (Tangent gas) all have a negative slope for dp/dv on the p-v diagram and therefore have positive adiabatic wave speeds.

For compressive waves, the classical or exact wave equation, expressed in terms of the wave function ψ for amplitude, is [9]

Ѳ ψ = 1/c² ∂²ψ/∂t² [ 1 + Ñψ ]^{(k + 1)}

or, for one dimensional motion in the x-direction

∂²ψ //∂x² = [(1/c²) ∂²ψ /∂t² ]/ [ 1 + ∂ ψ /∂x ] ^1+k.

This exact equation means that, for real or material gases ( k > 0), compressive waves are always unstable and grow with time . For very small amplitude waves however, the term in the denominator involving 1 +∂ ψ /∂x approximates to unity, and the equation simplifies to become the classical wave equation of very low amplitude sound waves (acoustic waves)

Ѳ ψ = (1/c² )∂²ψ/∂t²

which has the general solution

ψ = ψ₁₍x – ct) + ψ₂ ( x – ct)

In the case of the UF, however we see that, since k = – 1, the exponent ( k + 1) of the denominator term becomes zero so that the term itself becomes unity , thereby automatically reducing the equation to the simple classical wave equation, but without any of the approximation needed for real gases such as air.

The UF is unique in that it alone is automatically exact for waves of any amplitude, large or small, that is to say it is no longer limited to infinitesimal waves as is the case with real gases. The UF is therefore unique among gases, since in all real gases finite amplitude waves always either steepen or die out, and only sound waves of infinitely low amplitude (i.e. acoustic waves) can persist as stable waves.

The natural representation of the solutions to the classical wave equation

ψ = ψ ₁x – ct) + ψ ₂( x = ct)

is on the (x,t), or space-time diagram. Figure 3 shows the characteristic lines representing two families of left-running and right-running waves on the space-time or ‘physical plane’ diagram.

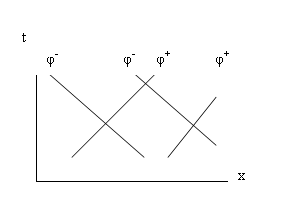
Figure 3. Space-time( physical plane) Plot of 1-dimensional

Wave Characteristic Lines

The fact that these characteristic solutions of the classical wave equation ( i.e. of the UF) are linear and can be superimposed directly relates waves in the UF to quantum physics and wave mechanics.

3.2.5. Wave speeds in the UF

For isothermal motions ( i.e. constant temperature, ∆T = 0), we have the isothermal (Newtonian) speed of sound waves in a perfect gas

c² = pv = p/ρ = RT ; c = [pv]^1/2.

Now in the UF where k = −1 we have:

a) The Tangent ( i.e. adiabatic, constant heat , ∆Q = 0 ) Equation of State :

p = −Av + B

The general adiabatic sound speed equation is c² = kpv, therefore, in the Tangent case with k = − 1, we must have

c² =k pv = k [−Av² +^-Bv] = +Av² − Bv

and the sound wave speed c is positive as it should be.

b) Our isothermal equation of state is: p = +Av − B

The wave speed in an isothermal gas is given by c² = pv, and therefore we must have

c² = pv = v[+Av − B] = +Av² − Bv

Therefore, since the right hand side of the equation is positive, the isothermal state also appears to have a positive wave speed so long as B is less than A . However the usual derivation of c² = dp/dρ gives us dp/ dρ= d(+Av –B) / dρ = d(+A/ρ − B) / dρ = −A/ρ² = c² so that here c² is negative and the wave speed c involves the imaginary i, which suggests damped oscillations only, instead of waves. The problem appears to centre around the required negative slope of the curve on the p-v diagram for a positive wave speed in Quadrant 1.

3.2.6. Isentropic ratios ( c, p, ρ, T) and relative motion (V)

The general isentropic ratios relating pressure, density and temperature for any ideal gas, are ( using n = 2/(k-1))

c/c_o = [p/p_o]^1/(n+2) = [ρ_o/ρ]^1/n = [T/T_o]^1/2

In the UF where k = − 1 we see that n =2/(k – 1) also is equal to − 1, and these isentropic ratios then become

c/c_o = p/p_o = ρ_o/ρ = v/v_o = [T/T_o]^1/2

but, while this is so for the isothermal gas, it is not so for the adiabatic or Tangent gas because of the negative slope of the latter equation of state on the p-v diagram. Careful analysis is needed on this point. For the Tangent gas the isentropic ratios are

p/p_o = [−Av +B] / [−Av_o +B] which for the special case where B = A = 1 is approximately given by

p/p_o = ρ/ρ_o = v_o/v

The energy equation for relative motion V with k = n = − 1 becomes

c/c_o = [ 1 + (V /c_o)² ]^1/2

Therefore, we also have

p/p_o = [1+ V²/c_o² ]^1/2

p/p_o −1 = ∆p/p_o = [1+ V²/c_o² ]^1/2 − 1

∆ρ/ρ = [1+ V²/c_o² ]^1/2 − 1

relating pressure pulses ∆p, and corresponding density pulses ∆ρ to relative fluid motions V in the UF, for example to oscillations of an electric charge or accelerations of a material particle.

The various possible types of wave motions can then be investigated by imposing (a) condensation pulses ( +∆ρ), (b) rarefaction pulses (−∆ρ) and (c) density oscillations ( ± ∆ρ) as in Fig. 4.

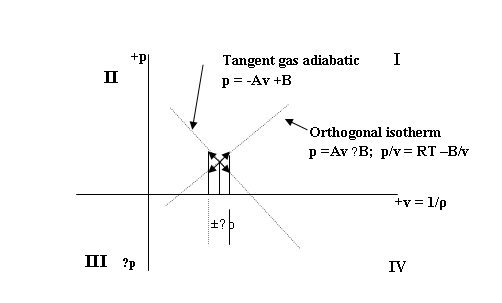
Figure 4. Density Perturbations and Wave Motion in the Universal Field

Figure 5. Various Wave Motions in the UF

3.2.7. Stagnation Values of Pressure, Temperature and Density for the UF

In any compressible field the basic initial values of interest are often those when there is an adiabatic reduction to a state of no fluid flow ( V = 0). These are called the stagnation values and are designated as p_o, T_o and ρ_o . Their numerical values for the UF remain to be determined.

So far we have not distinguished between longitudinal and transverse wave motions in the UF. Clearly there is no problem with longitudinal waves; they are uniquely supported in the UF, and, moreover, they are not restricted to low amplitude acoustic type waves as in real gases where k is positive. We shall now present evidence that transverse waves are also uniquely supported in the UF, and that they in fact correspond to Maxwell’s electromagnetic waves which transmit light and other radiation through space.

Real gases, being tenuous fluids, can only support longitudinal waves, that is to say, waves in which the density variations ±∆ρ are along the direction of wave propagation. They cannot support transverse waves in which the density variations would be transverse to the direction of wave propagation. It was this inability of a tenuous medium to transmit the transverse waves of light which led to the demise of the old luminiferous ether concept. We now ask: What is the evidence for transverse fluid waves in the Universal Wave Field (UF ) with its mutually orthogonal adiabatics and isotherms?

3.2.8. Evidence for transverse waves in a tenuous fluid

We consider a simple pressure pulse ( ±∆p) in the UF as in Fig.6 below:

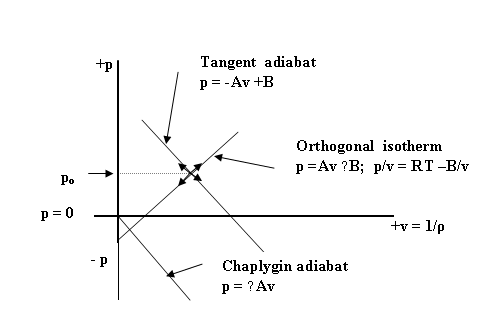
Figure 6. A pressure pulse ( ±∆p) in the Orthogonal Environment of the UF

The initial or stagnation state is designated as p_o. When the pressure pulse ( +∆p) is imposed from outside in some way, the UF must respond thermodynamically in two completely orthogonal, and hence two completely isolated ways, namely, by (1) an adiabatic stable wave along the adiabatic( TG) and (2) by an isothermal stable pulse along the isotherm (OG).

Spatially, the pressure disturbance ( +∆p) must propagate in the direction of the initial impulse. But, since the two components of the pulse are orthogonal, they must still remain completely independent and physically isolated. The only way possible for this to take place is for the two mutually orthogonal components to also be transverse to the direction of propagation of the two pressure pulses. This requires an axial wave vector V in the direction of propagation ( say z), and with the two pulses orthogonally disposed in the x-y plane. i.e. TG x OG = V which is reminiscent of the Poynting energy vector S = E x B in an electromagnetic wave.

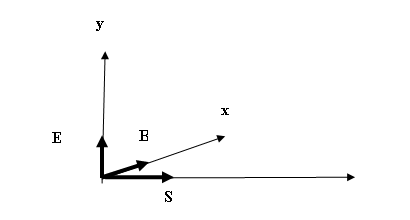Figure 7. Electromagnetic Poynting energy /vector

A wave of amplitude ψ traveling in one direction (say along the axis x) is represented by the unidirectional wave equation

dψ/dx = 1/c dψ/dt

3.2.9. Maxwell’s electromagnetic waves

Here, however, in the case of our adiabatic and isothermal pressure pulses we have two coupled yet isolated unidirectional waves, and this reminds us of Maxwell’s coupled electromagnetic waves for E and B, as follows

dE_y/dx = (1/c) dB/dt and dB_y/dx = (1/c) dH/dt

where c is the speed of light, E is the electric intensity and B is the coupled magnetic intensity.

Maxwell’s E and B vectors are also orthogonal to each another and transverse to the direction of positive energy propagation.

Therefore, we have established in outline a two component wave system in the Universal Field (k = −1) which formally corresponds to the E and B two component orthogonal system of Maxwell for electromagnetic wave propagation through space in a continuous medium. His equations for E and B are

Curl E = ∂E_y/∂x = −(1/c) ∂B/∂t

Curl B = ∂B_y/∂x = − (1/c) ∂E/∂t

If we now designate our Tangent gas as A ( for Adiabatic) and our Orthogonal gas as I ( for Isothermal) then our analogous wave equations would be

Curl A = ∂A_y/∂x = − (1/c) ∂I/∂t

Curl I = ∂I_y/∂x = − (1/c) ∂A/∂t

The two systems are formally identical. Therefore, we propose that the medium in which Maxwell’s transverse electromagnetic waves travel through space is to be physically identified as a Universal Compressible Field (UF) having the above described thermodynamic properties for adiabatic and isothermal motions initiated in the UF by imposed pressure pulses ( presumably by accelerated motions of electric charges). The compressibility of the UF now properly accounts on physical grounds for the finite electromagnetic wave speed (speed of light), and in addition, wave motions in this tenuous fluid medium are transverse, as required by the observations..

It is possible to reduce Maxwell’s two equations UF equations to a symmetrical single wave equation

∂²E/∂x² = (1/c²) ∂²E/∂t²

∂²B/∂x² = (1/c²) ∂²B/∂t²

and similarly with A and I for our Adiabatic/Isothermal coupled wave in the UF:

∂²A/∂x² = (1/c²) ∂²A/∂t²

∂²I/∂x² = (1/c²) ∂²I/∂t²

This is not surprising since the UF with its k = −1 thermodynamic property is the unique compressible fluid which automatically generates the classical wave equation with its stable, plane waves. The formal agreement of the UF theory with Maxwell is striking.

Instead of taking our initial external perturbation as a pressure pulse ( +∆p) we could more realistically from the physical standpoint take it to be a density condensation (s = ( ρ – ρ_o ) / ρ_o = +∆ρ/ ρ_o). This will now result in a positive pressure pulse (+∆p) appearing in the adiabatic (TG) phase of the UF but a negative pressure pulse ( −∆p) in the isothermal or orthogonal perturbation component (OG) . This perturbation is represented by the two orthogonal sets of arrows on the pv diagram, one corresponding to +∆p and the other set corresponding to − ∆p. As the wave progresses the two orthogonal vectors also rotate.

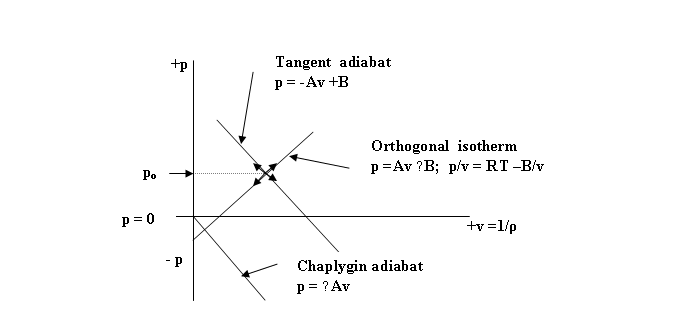
Figure 8. The physical ambiguity which results from a pressure/density perturbation in the Orthogonal UF

Therefore, an oscillating density perturbation ( ±∆ρ) results in an axial wave vector having two mutually orthogonal components ( adiabatic and isothermal ) in a density perturbation wave. This appears to correspond formally to the Maxwell electromagnetic wave system with its two mutually orthogonal vectors for electric field intensity E and magnetic field intensity B.

We have thus established a case for the compressible UF being a cosmic entity which transmits transverse electromagnetic waves through space. A necessary next step will be to examine the UF in relation to all the multifarious established facts relating to electromagnetic radiation.. These must include the nature of electric charge, electrostatic fields, the compressed fields of moving charges and resulting magnetic fields, etc. etc. Preliminary work has indicated that this additional reconciliation will be successful.

3.2.10. Polarization and Spin

Since we are dealing here with two linked mutually orthogonal states, all the formal requirements of electromagnetic polarization and spin are automatically satisfied. Various other physical details remain to be examined by specialists.

3.2.11. Electromagnetic Wave Quantization: Photons and the Orthogonal State Waves

Perhaps a bit simplistically, we could just consider each individual axial vector wave as single basic wave entity or quantum entity and then build up more complicated energetic states by superposition of the basic linear waves. That is to say, we could consider each individual perturbation a quantum. But we would still have to explain the basic energy quantum relation e = hv.

However, the quantization can perhaps also be seen on a more physical basis, if we set the UF’s stagnation or rest pressure p_o at some small value very close to p = 0, say at p_o = 6.673 x10^-11 kilopascals. This at once makes the maximum allowed value of any negative pressure perturbation −∆p equal to 6.67 x10^-11 kpa as well, because, if only symmetrical pressure perturbations ±∆ρ are allowed to transmit waves, that is, if only equal amplitude perturbations are permitted , then the waves would be quantized at the maximum amplitude set by −∆p equal to 6.67 x10^-11 kpa,( so long as p = 0 is the lowest pressure permitted, i.e. so long as negative absolute values of the pressures are excluded).

This quantization procedure is also applied to gravitation in a succeeding section.

3.2.12. Special Relativity: The question of whether the UF proposal reintroduces a cosmic “medium” into space will also eventually come up, although it is more a matter for experiment to settle than for theory. Perhaps all that need be said at this point is that when the relativity of motion is investigated with respect to the new UF field proposal, the laws of compressible flow must be applied. In compressible flow all velocities are physically purely relative, and, as shown above the compressible energy equation yields the Lorentz/Fitzgerald transformation in a more general form than special relativity, and now on physical grounds. In the matter of the central problem of relativity, which involves the direct mathematical addition of material source velocities to the velocity of light, the addition formula from compressible theory containing the energy partition parameter n must be used, instead of the failed classical direct addition of velocities that led to special relativity being introduced in the first place.

To repeat for clarity in this matter, the new addition rule will involve (c ±V/√n) where n = 2/(γ–1), instead of the old classical (c ± V). This is because it derives from the kinematic energy flow equation

c² = c_o² – (1/n) V²

and we get the ratio of wave speeds

c/c_o = [ 1 – V² / n c_o² ]^1/2

which sets the correct velocity addition formula for compressible flows. We see that it involves the introduction of the energy partition parameter n ( n = 2/k – 1). This formula is just the familiar Fitzgerald/Lorentz contraction factor with the addition of the parameter n. In most cases this addition of n greatly reduces the expected fringe shifts and oscillation changes that are theoretically predicted by the old failed classical formula and it bring them into line with the magnitude of the perturbations that are observed in experiments designed to detect uniform or absolute motion through space. For details, see a current review of the observational data of the Michelson-Morley and later experiments at www.energycompressibility.info /Appendix A: Relativity and Results of Michelson-Morley Type Experiments.

Some of the formulae of the Lorentz transformation, and hence of special relativity, are directly related to the above formulae for compressible flow for the special case of n = +1 ( k = 1.67) in experiments such as those on the apparent increase of mass with velocity in accelerators. However, in general, the value of n for any given experiment is not unity, but must be properly determined or estimated, since an experiment involves not just the wave transmitting field but the interaction of the material apparatus and all relative motions and accelerations. For the Michelson-Morley apparatus, for example, the value of n seems to be about 9, for the atmosphere it is 5, for combustion gases it is close to 9, and for high speed accelerators it is close to 1.

But in compressible flow in the UF, Lorentz invariance becomes an approximation which is valid only for low fluid velocities. For higher relative velocities near the critical wave speed ( c* , Mach 1) the kinematic energy equation must be applied, since in compressible flow the wave speed c is a physical variable for both compressive waves and transverse ( electromagnetic ) waves.

3.2.13. Summary of Transverse Waves in the UF. Maxwell’s electromagnetic field equations involve two mutually orthogonal field vectors E and B which obey the classical wave equation and form a transverse wave propagating in space. Maxwell’s system is a complete and self-consistent theoretical structure which then agrees with the facts of experiment. The UF is the only known theoretical field ( k = n = −1) which can support classical wave motion without approximation, and which furthermore involves two mutually orthogonal field vectors A and I which can form and support a transverse wave propagating in the UF through space. The two systems are formally identical, and, since Maxwell’s equations are fully verified by experiment, then the UF system is also thereby verified.

Finally, with the UF taken as a unique, compressible fluid medium which transmits transverse electric and magnetic waves, then the question naturally arises: Can the compressible UF also account for the unique nature of, and the spatial transmission of, the force of gravity? This is discussed next.

For a more detailed treatment of some aspects of this section see ( www.energycompressibility.info and www.shroudscience.info at the Page entitled Properties of a universal wave field.

3.3 (I) Gravitational Force and the Universal Field

3.3.1. Characteristics of Gravitation: The principal characteristics of gravitational force to be properly accounted for in a new theory are (1) its exclusively attractive nature for mass, (2) its extreme weakness relative to the electromagnetic force, and (3) its 1/r² decline in strength with distance. Newton’s formulation avoided any speculation as to the physical nature of the gravitational force and the manner of its transmission through space between material bodies. General relativity is based on the postulate of the existence of a geometrical space-time continuum; deformations in this continuum then constitute force, which is interpreted as being a deviation from linear motion.

Any new, physically based theory attempting to explain the nature and behaviour of gravitation will obviously have to account for the three physical characteristics set out above. It will not have to meet the general relativity postulates, but it will eventually have to explain why the latter theory does make successful predictions which offer corrections to the Newtonian predictions, such as the advance in the perihelion of Mercury, and various gravitational lensing effects on light waves.

3.3.2. Exclusively attractive forces in the Universal Field

In any compressible fluid, force is given by the Euler equation , which for 1-dimensional flow is

F = ∂u/∂t + u ∂u/∂x + v ∂u/∂y +w ∂u/∂z = −(1/ρ) ∂p/∂x,

where the term on the right hand side is called the pressure gradient force.

In any compressible fluid medium, waves set up local transient pressure gradients and so forces arise. Most waves in real gases and fluids are pressure oscillations (±∆p) and so they do not exert any net directional force on a material object they encounter. However, in the UF special types of waves can occur which can be either exclusively pressure compressions (+∆p) thereby exerting a net repulsive force on any material body in their path, or they can be exclusively pressure rarefactions (−∆p) which would then exert exclusively attractive force.

Consider Figure 9 where an isothermal condensation pressure pulse (+∆ρ; +∆ρ) imposed on the initial stagnation pressure p_o in the UF will produce a rarefaction pressure pulse (−∆ρ) in the isothermal mode of response. Consequently, a source of pressure condensations will produce a train of isothermal rarefaction pressure pulses as a response in the UF, and these pulses will travel spherically outwards through space.

When these rarefaction waves eventually impact a material body (mass) they will exert a net attractive force on it. This mechanism, therefore, in simple outline is formally equivalent to the force of gravity being produced by a rarefaction pressure gradient force.

Figure 9. Positive density pulse ( +∆ρ) of any magnitude produces a quantized gravitational isothermal rarefaction pulse (−∆p_g ) of constant magnitude p_g =6.67 x 10^-11 kilopascals

3.3.3. Extreme Weakness of the Gravitational Force and the Universal Field

The three main forces in nature are the strong nuclear force, the electromagnetic force and the gravitational force. The nuclear force is very much the strongest. The electromagnetic force is about 1/137 th of the nuclear force. The force of gravity, however, is extraordinarily weaker that the other two, being only about 10^-40 th. the strength of the electromagnetic force. Thus we have

F_s / F_e/m = 1/137 ; and F_g / F_e/m = 10^-40.

We have shown above that a wave train exclusively made up of pressure rarefactions would explain the attractive nature of gravity. Now we must explain how these rarefaction waves can all be so extremely weak.

Consider, again, a positive density pulse (+ ∆ρ) imposed on the UF. (Fig. 9). Adiabatically this will result in a pressure increment (+∆p) , but in the isothermal mode this will give a pressure rarefaction (−∆p).

We must now consider whether a sufficiently large negative pressure pulse (−∆p) can transmit in the isothermal mode right through the p = 0 expansion and on into the negative pressure region of Quadrant IV. It appears that it cannot, because of the fact that a negative pressure will entail a negative temperature, and quantum theory and experiments all show that temperatures of opposite sign are not equal in magnitude [a, b, c] Thus the isothermal condition will be discontinuous on the v-axis at the p = 0 point. Physically this appears to require that the negative pressure pulse must terminate at this point. The consequence then is that all negative isothermal pressure pulses will be truncated to some maximum amplitude.

(−∆p) _isothermal = ( p_o – 0) = p_g – 0 = constant = 6.67 x 10^-11 kilopascals.

Therefore, if the initial pressure/density perturbation is inserted into the UF at its static pressure p_g = 6.67 x 10^-11 kpa, then the induced negative isothermal pressure rarefaction (−∆p ) will be (a) extremely weak and always of the same maximum amplitude of 6.67 x ^10-11 kpa. no matter what the amplitude of the initiating positive density pulse (+ ∆ρ).

Again, we have F_g = − v dp/dx = − 1/ ρ dp/dx . Therefore, for unit mass at unit distance we have F_g = − ∆p = G = 6.673 x 10^-11. Thus the basic UF stagnation pressure p_o seems to correspond numerically to G, the gravitational constant, as we have just postulated (p_o = 6.673 x10^-11 kilopascals).

On this physical model, gravitational force is carried through space isothermally by a train of rarefaction pressure pulses (−∆p), all physically constrained to have the same invariant maximum amplitude regardless of the amplitude of the initiating positive density pulse (+ ∆ρ).

Then to show that our gravitational formulation gives the required weakness for the gravitational force, consider Newton’s force formula

F_ig = (G m₁ m₂) / r²

and the Euler pressure gradient force

F_p.g = −1/ρ (dp/dx) = −v (dp/dx)

If we now take dp = lGl and, realizing that the equation is for unit mass ( m = 1) , we get (at unit distance dx = 1) the force

on a unit mass F_g = − (1) 6.67 x 10^-11 Newtons. For the force on a single proton ( mass = 1.67x10^-27 kg) we would then have

F_g = 1.67x10^-27 [ 6.67 x 10^-11] = 1.1x10^-37 Newtons,

which reconciles the new UF force formulation with the Newtonian predictions.

3.3.4. A Unique Wave Speed Assciated with Gravitational Waves

In general, in the UF the wave speed, given by c² =(3 x 10⁸)² = ∆p /∆ρ holds, and the wave speed c is the speed of light in space. However, consider what happens when in the generation of a gravitational wave pulse as just described above, the reduction in p in the isothermal mode approaches the zero pressure point. At this point, if the wave pressure action then cannot continue on into negative values of p in Quadrant IV as required by the magnitude of the initiating positive pressure pulse , then we have the UF fluid approaching a state where v = 1/ ρ = constant and so any additional ∆ρ needed must become zero. But then the gravitational wave speed must approach infinity since c² =dp/ 0 must then equal infinity.

As to the probable magnitude of this new gravitational pulse wave speed we propose the following: The ratio of the gravitational constant to that of the Planck constant is

G/h = 1.04 x 10 ²³ = constant

If mass is taken as dimensionless ( as we do everywhere in this theory on the grounds that mass is a condensation of energies and so can be consider a ratio of energy before and after elementary particle formation ) then the dimensions of the ratio G/h are those of velocity or speed [l t^-1].

It thus seems possible that the ‘reflection’ of the positive pressure waves of Quadrant I at the p = 0 boundary or discontinuity may generate an additional transient, extremely fast UF wave as well as propagating the basic electromagnetic or gravitational pulses that it reflects and sustains. This new wave seems more likely to relate to the spread of quantum information through space rather than to the transfer of energy.

In summary, we have exclusively attractive gravitational waves traveling at the speed of light speed of light, but, as each wavelet reaches the zero pressure point ( p = 0) it emits a secondary wave which spreads spherically at quasi-instantaneous speed.

For a variety of reasons we also associate this secondary quasi-instantaneous pulse radiation with quantum wave information spread.

3.3.5. Quantum Information and the UF

While this very large and complex subject has not yet been reexamined in great detail, there are some aspects which already indicate that compressible flow and the UF concept are intimately related to quantum phenomena, just as has been shown above for electromagnetism and gravitation. Some of these will be presented Part II.

For a more detailed treatment of this section see (a www.energycompressibility.info) and (www.shroudscience.info and open the page entitled Properties of a Universal Wave field

3.3.6. Summary. We have shown that the UF can support and transmit stable rarefaction waves which (1) exert exclusively attractive force on masses and (2) have the necessary extreme weakness. This meets the general requirements for them being gravitational waves and for the UF therefore being the physical seat of universal gravitational force.

There are, of course, many other aspects of gravitation we have not considered here These also will have to be considered in light of the theory, but they are not essential for this general presentation.

Having shown that the UF is the source of radiation and gravitation, we are now in a position to proceed to examine its thermodynamics and show that its Carnot cycle forms the basis for a new cosmology. Then in Part II ( in preparation) we show that the UF Carnot cycle explains (1) the origin of the Big Bang, (2) the nature and origin of ordinary baryon matter, (3) the nature and origin of dark matter, and (4) the nature of dark energy so as to thereby construct a new general cosmology.

4.0 (I) COSMOLOGICAL ORIGIN AND THERMODYNAMIC EVOLUTION OF THE UNIVERSAL FIELD (UF) DURING A CARNOT CYCLE

4.1. Cosmic Origins: Initial postulate of the existence of a cosmic fluid

The proposed new cosmological model has one physical assumption, namely that at an initial cosmic time t_initial there existed a physical cosmic fluid continuum having pressure p_L, density ρ_L , temperature T_L, energy ε_L and tensile strength ∆p_L.

This postulated cosmic fluid has an equation of state of the general form pv^k = constant.

4.2 Initial Event: Cavitation or rupture of the cosmic fluid to form a vapour filled Universal Field (UF)

We now envisage the emergence and evolution of the Universal (vapour) Field (UF from the cosmic fluid as follows:

At initial time t_R a rupture of the cosmic fluid is postulated to have occurred at one point in the cosmic continuum (or possibly at many).

In most fluids rupture occurs at a tensile strength that is many orders of magnitude lower than the theoretical value [10,11,12,13]. In the course of studying the properties of the UF [14 – 25] the reason for this anomalous tensile strength was found to be described by a spherical compressible rupture mode [24 ]. Our initial rupture flow is therefore taken to be radial (i.e. spherical) and to obey the equation of state or expansion law pv⁷ = constant (k = 7; n = 1/3) [24].

In accordance with fluid bubble dynamics [10,11] this rupture event occurs when

∆p = const./ (∆V)⁷ = 2 σ /R_C

which gives the relationship between the initial (radial) expansion ∆V needed for the rupture to form the void, the interfacial surface tension σ and the rupture radius R_C .

4.3. (I). UF Carnot Cycle Step #1: Isothermal expansion of vapour filled bubble to critical sizeforming a Universsl Field

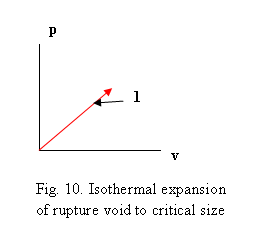The cosmic void or bubble next expands isothermally according to the Rayleigh-Plesset equation to reach its stable radius R [10,11].

(p_B – p_L)/ ρ_{L =} ∆p_∞/ ρ_L = R (d²R/dt²) + 3/2 (dR/dt)² + 2σ /R ρ_L

At the stable or critical size R_C this equation reduces to ∆p_∞. = 2σ /R_C.

During its expansion the cavity or bubble fills with vapour from the enveloping cosmic fluid continuum to form a universal cosmic vapor field (UF) of radius R_c. This UF is to be understood as physically real, and in it take place all the physical phenomena of quantum physics, uniform classical forces and motions, accelerated gravitational motions, and electromagnetic radiation phenomena, all of which are experimentally verifiable. In the course of study it was also found that the Carnot cycle energy in the UF is represented on the pressure-volume diagram by a rectangular area. Details are presented in Appendix A [23].

The UF has the physical properties enumerated above in section 3, which include:

Equations of State: We have shown above that in gas dynamics there is the so-called Chaplygin gas with adiabatic equation of state

hrough the origin :

pv^-1 = p/ρ = constant ;or

p = −Av

In Quadrant I this becomes the Tangent gas

P = −Av +B

The corresponding isothermal equation of state [ 23] Appendix A is

pv^-1 = const. or

in Quadrant I

p = +Av − B

These equations taken together constitute the equations of state for our Universal Field.

In the case where the isotherm starts at the point of origin (p = v = 0) the isothermal equation reduces to

p = Av = A/ρ, so that its expansion obeys

p₁/p₂ = v₁/v₂ = ρ₂/ ρ₁ which is basically the inverse of that for the Chaplygin/Tangent gas.

The unusual properties of the UF are re-stated as follows:. (1) It uniquely supports stable waves of any amplitude both in compression and in rarefaction which obey the classical wave equation; (2) Although it is a tenuous fluid or vapour, it uniquely supports transverse waves which are identical to Maxwell’s electromagnetic equations; (3) Its compression waves are uniquely attractive in nature and correspond to the requirements for a wave disturbance carrying gravitational forces through space. This ‘graviton gas’ forms the basis for a quantum gravity; (4) It supports waves corresponding to the de Broglie wave/particle equation and thus relates to the quantum wave function and the transfer of quantum information through the cosmos; (5) Its isothermal expansion is shown to be the possible source and origin of the so-called ‘dark energy’, thus furnishing a physical explanation for the observed increased rate of acceleration in the expansion of the universe [6,7,8].

Its state equations are graphed in figure 11.

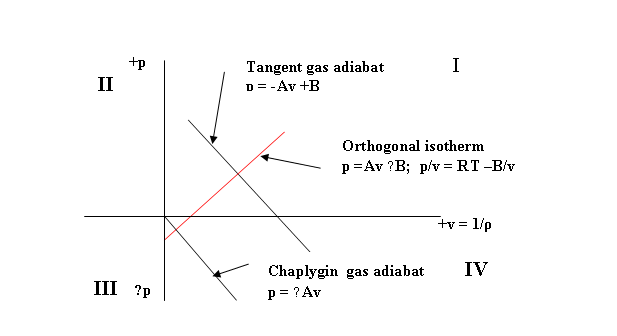
Figure 11. Equations of State for the Universal Field (k = − 1; pv^-1 = const.)

4.4. (I) UF Carnot Cycle Step #2. Adiabatic collapse of the UF to a state of high energy and compression

(A) Collapse: The bubble filled with the newly generated graviton gas field having reached the critical radius now collapses. This bubble collapse generates an enormously increased pressure, density and temperature [10,11 ]. The pressure increase ratio is roughly proportional to the ratio of the initial radius R_C to the final compressed radius or R_C/R_F

p = 100R_C/ R_F

This adiabatic compression of the (UF) tangent gas obeys the compression ratio law

p_1/p₂ = [−Av₁+ B ]/[ −Av₂ +B] , but, since A and B are not known, no numerical solution can be attempted without assumptions. If we assume that A= B = 1 we get the approximation

p_1/p₂ = [−v₁+1 ]/[ −v₂ +1]

4.5. (I) UF Carnot zCycle Step #3: Isothermal further compression towards the Big Bang: TheFormation of Matter

In this step the UF compresses isothermally following the same laws as for Step 1 of the Carnot Cycle given in Section 4.3 above. A logical question here is: Why does the expansion change from adiabatic to isothermal?

In Part II ( in preparation) we shall present the evidence that ordinary particulate matter precursors e.g. quarks, are formed by compression ate the turning point to Step 3, and that they then subsequently aggregate, as for example in the Standard Model of Big Bang expansion, to form the atoms of our evolving physical world. It seems reasonable to assume that it is this condensation or phase change that triggers the change from Step 2’s adiabatic compression and volume collapse to Step 3’s isothermal decompression and continued volume collapse leading to the Big Bang state. We point out here that with many vapours, condensation take place not upon expansion but upon compression and heating. Many organic vapours, such as those of turpentine for example, condense upon compression. The latent heat of condensation L offers a criterion as to which process occurs. For example, the condition that the ratio of latent heat L to temperature T is

L/T > (c_p− c_v) k/(k−1)

means that condensation in that particular vapour takes place upon adiabatic expansion. Whereas with the condition

L/T < (c_p − c_v) k/(k−1),

condensation would requires compression. The criterion obviously is whether L is large or small compared to T. The latent heat of condensation of water vapour, for example, is large ( 540 cal/g) and water vapour condenses to liquid upon expansion of its vapour. A latent heat of around 100 cal/g, for an essential oil such as pinene, would mean condensation from the vapour to liquid upon compression. Consequently the proposal that World A particulate matter was formed by compression just before the Big bang is physically possible. Evidence that this is the case will be contained in Part II, currently in preparation and will be posted on this website as Part II: Origin and Evolution of Matter, Dark Matter and Dark Energy when available].

We propose setting R_F, the radius of the cosmos at the Big Bang compression ( the completion of Step 3) equal to the Planck length ( R_Pl = 1.3x10^-35 m). Then, if we surmise that the pressure at the end of collapse is, say, the present day estimated value of the quantum vacuum or 10¹²¹ kPa, we get the size of the UF bubble before collapse to be about 10⁸⁵ m. This is 10⁵⁹ times the radius of the present day observable universe of ordinary matter which is about 10²⁶ m .

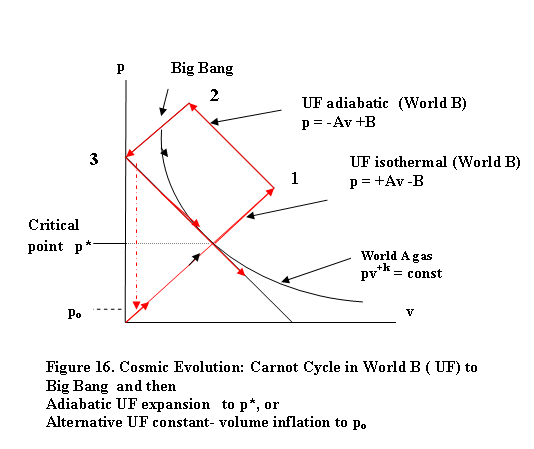
Continuing on in the Carnot cycle to the enormous explosion of the Big Bang, we are presented with two choices : (a) an adiabatic expansion of the UF after the Big Bang instant or (b) a sudden constant-volume loss of pressure in the UF as a consequence of the condensation of its quark plasma into the substance of ordinary World A matter.

4.6. (I) UF Carnot Cycle Step # 4: Two choices: (a) Adiabatic expansion of the UF following the Big Bang or (b) Sudden constant volume pressure loss in the UF during the formation of particulate matter (quarks) by condensation

In the general relativity model of cosmology, the post-Big Bang expansion is modeled using the Friedman dynamic equation. Here, we also could make the expansion from the Big Bang moment to the present cosmic time with the Rayleigh-Plesset equation which is formally quite close to the Friedmann equation. Both of these, however, are differential field equations, and, as pointed out, they suffer from the drawback that they require a knowledge of boundary conditions for a definite solution, while, of course, the boundary conditions of the cosmos are unknown. Furthermore, they cannot really handle singularities such as the Big Bang and the existence of the elementary particles of matter, and so these components of the universe must be inserted ‘ by hand’ so to speak.

In the present theory on the other hand we start not with differential equations with undetermined solutions but with an integral equation yielding a single definite solution. Our integral field is an Equation of State of a compressible fluid field, for example, the adiabatic equation for an ideal gas (pv^k = const), or in the present case the Tangent gas with k = n = − 1 i.e pv^-1 = p/ρ = const.

The general isentropic expansion ratios which relate pressure, density and temperature for any ideal gas, are (using n = 2/(k-1)):

c/c_o = [p/p_o]^1/(n+2) = [ρ_o/ρ]^1/n = [T/T_o]^1/2.

In the UF with n = − 1 we might therefore think that this would just become

c/c_o = p/p_o = ρ_o/ρ = v/v_o = [T/T_o]^1/2

but we must realize that the UF has two orthogonal equations of state, one with negative slope on the p-v diagram, namely the adiabatic or tangent gas with positive wave speed, the other the isothermal state with positive slope and probably imaginary wave speed.

For the adiabatic expansion of the UF( i.e. tangent gas) we must use

p₁/p₂ = v₂/v₁ = ρ₁/ρ

so that the pressure volume relationship is an inverse one.

For an isothermal expansion we have

p₁/p₂ = v₁/v_2. = ρ₂/ρ₁

where the pressure and volume change in the same sense and it is the pressure-density relationship that is now inverse.

a) Choice #1: Adiabatic expansion of the UF after the Big Bang

The adiabatic expansion ratios for the UF are p₁/p₂ = [−Av₂ +B]/[ −Av₁ +B].

Since A and B are presently unknown we cannot use this formula to make numerical estimates to compare with any known thermodynamic values. But, if we were to assume, for example, that A = B = 1 we could get an approximation p₁/p₂ = [v₂+1]/[v₁+1], and therefore, the expansion from the Big Bang (p,v)_N to the present time (p,v)_N would be approximately p_B = p_N [v_N] , since v_B is so very small that v_B+1 is effectively equal to 1.

With this assumption and taking p_B= 10¹²¹ and v_N = 9.2 x10⁷⁸ m³ we get p_N =1.1x 10⁴² kPa which makes little physical sense.

Even if for v we compute the specific volume v = 1/ρ from an assumed density of 1 atom per cubic meter, which is a currently used theoretical value, i.e. v_N = 1/ρ_n = 6x10²⁶, then we get p_N = 1.64x10⁹⁴ kPa. These two values give us pv =10¹²¹ kPa by definition, but the UF pressures cannot be assessed against present physical data. We therefore tentatively conclude that the expansion in the UF from the time of the Big Bang to the present time, while it may have been adiabatic, does not yield any obviously simple correlations with known physical data and so is problematical.

b) Choice #2: Sudden constant-volume pressure loss in the UF during the formation of particulate matter ( quarks) by condensation followed by an Isothermal expansion to the present day.

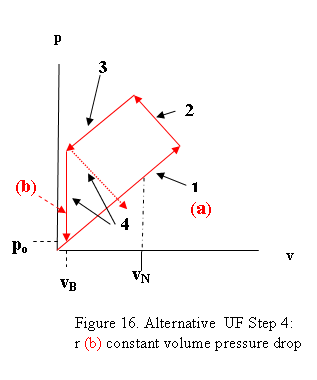wever, instead of the above adiabatic expansion of the UF after the Big Bang Figure 15 , we can envisage an alternative expansion which has the interesting quality of providing a physical explanation for inflation. This step would be a sudden constant-volume drop in pressure in the UF, perhaps as a physical consequence of the sudden formation of the World A’s ordinary matter of protons, neutrons, etc. by condensation from the quark plasma of the UF. Fig. 16(b).

This collapse of UF pressure would then release the enormously compressed plasma of World A matter into the sudden massive expansion proposed by inflation theory [28] as an explanation for the observed, overall, quasi -uniformity of the cosmos in contrast to the presence of the galaxies and stars.

Our proposed UF pressure drop is taken as occurring at constant volume from the Big Bang value (10¹²¹ kPa) down to the value p_o = 6.67x10^-11 kPa ( Fig. 16), which is our postulated stagnation pressure of the UF for reason discussed above in Section 3.3 on gravitational force.

The expansion ratios for the isothermal state in UF taken through the origin are, as given above

p_B/p_N = v_B/v_N.

Using this ratio we can expand the UF isothermally from v_B =9.26x10^-105 m³ and p_o = 6.67x10^-11 kPa to estimated present day values of v and p as follows:

Initial UF values after inflation: v_o = v_B = 1.08x10^-104 ( Planck volume)

p_B = 6.67x10^-11 ( assumed)

UF values after isothermal expansion: Volume(actual) = 9.2x10⁷⁸ m³⁽ (Calculated from radius of cosmos at 13.7 billion years )

Calculated UF Pressure Now: p_N = p_Bv_N /v_B = 6.67x10^-11 x 9.2 x10⁷⁸ /9.26x10^-105 = 6.6x10¹⁷²

Or, using specific volume Now v_N = 6 x 10²⁶ = we get

Calculated UF pressure Now: p_N = p_Bv_Nsp/v_B = 6.67x10^-11 x 6x10²⁶/ 9.26x10^-105 = 10¹²¹ .

In effect this would mean that the UF, since inflation, has expanded isothermally to around its original Big Bang pressure. This is a rather unexpected finding.

We find that the hypothesis of an isothermal expansion of the UF down to the present day, following the Big Bang inflationary adjustment, is roughly supported by the data.

The next question is How would such a UF catastrophic pressure drop in inflation and subsequent expansion affect the companion field of our ordinary World A matter of atoms and molecules embedded in it?

Figure 16 shows one possibility, namely a smooth adiabatic expansion of World A matter from the Big Bang down to the present time.

There is however the more likely possibility that the UF inflation also caused a brief inflationary expansion of World A ordinary matter as well. This was followed by an adiabatic smoother expansion to the present day condition as depicted in Figure 17 below:

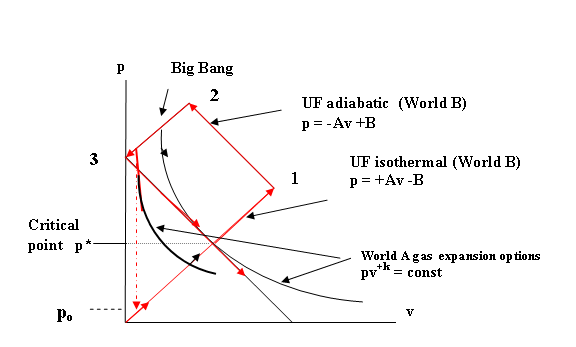
Figure 17. World A expansion from Big Bang with initial inflationary phase followed by adiabatic expansion

4.7 (I) Critical Point Intersections of the UF and World A Expansion Curves

We have several points not yet addressed. (1) There is the formation of our physical World A of condensed matter particles – atoms and molecules- in the Big Bang and subsequent expansion to the present time which is examined in Part II.

(2) There is the fact that at the Critical Point C (Fig. 16) the rates of change of all parameters ( dp/dv, dp/dρ, dv/dte, dρ/dt, etc ) are now uniquely identical and so some physical processes may now proceed which were previously impossible or improbable. The peculiar possibilities arising from the rate- of- change singularity ( Point C*) may also be of interest to evolutionary biology since they could possibly mark a point of high probability for the emergence of life.

(3) There is the possibility of different phase transformation from World A matter to World B matter ( A- to- B transformation ) taking place at the Critical Point p* (Fig. 16) which may be related to the problem of the nature and occurrence of the so-called ‘dark matter’ in our cosmos which is currently thought to make up some 24% of the total mass-energy. This possibilitywill be explored in Part II to follow.

4.8. (I) Current accelerated isothermal expansion of the UF: Dark Energy ?

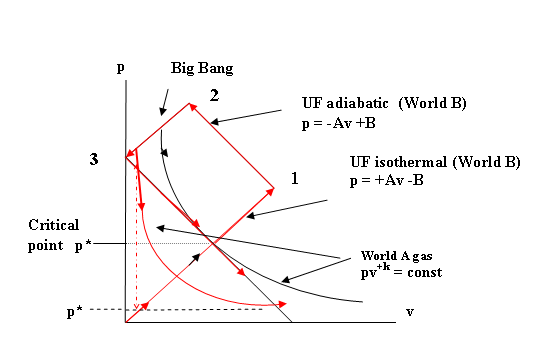
If the UF, at the Critical Point p* (Fig. 17) were to continue in an isothermal expansion it would, in effect be retracing its original path in Step 1. This increase in UF energy might explain or be related to the problem of the recently observed accelerated expansion of the cosmos and the so-called ‘dark energy’ which has been proposed as a solution [6,7,8].

This completes our present exploratory cosmology for the Binary Universe of World A plus the UF, so far as the Carnot Cycle of the UF is concerned.

Fig. 18. Summary of UF and World A evolutionary possibilities

and Critical Point Intersections

4.9.(I) Summary

Based on a standard physics of compressible fluid flow, the concept of a binary universe consisting of ordinary matter and the UF has provided a number of fundamental new insights that argue for its validity. It is based on only one physical assumption.

Starting with this single unifying postulate of the existence of a compressible fluid field, the origin and evolution of a Binary Cosmos has been presented, first the emergence of the of the tenuous vapour field of the UF in a fluid rupture and isothermal Carnot expansion, then its adiabatic collapse generating the enormous concentration of energy at the Big Bang, and forming the baryons of ordinary matter, then the Big Bang expansion and evolution of atomic matter, and then either (a) a continuation of the UF Carnot cycle in an adiabatic expansion towards the present cosmic time, or, more likely, (b) a sudden inflationary episode followed by an isothermal re-expansion.

The dynamic and thermodynamic properties of the UF - a development of the Chaplygin/Tangent gas – have been explored. It is seen to constitute a unique wave and force field with the ability to account for the transfer of electromagnetic radiation through space and to explain the origin and transfer of gravitational force through space.

The present cosmos is envisaged as being a Binary Universe, a co-existing dual entity consisting of ordinary matter and the co- evolving dynamic UF wave and force field. In Part II (under preparation) the origin of matter, the origin of dark matter and the nature and evolution of the dark energy will be examined.

The field equation of the UF is an integral equation of state which permits a unique solution with boundary conditions being the total dynamic energy ( enthalpy) of the universe.

It provides an explanation for the origin of both electromagnetic radiation and gravitational force and their transmission across cosmic and local space. Moreover, this concept is verifiable experimentally with optical and other means.

It provides [Part II, in preparation] an explanation for the origin of ordinary matter as being a condensed energy state arising out of an enormous compression of energy which started the Big Bang, and which, in its subsequent expansion and evolution after the Big Bang, accommodates the successful Standard Model of particle physics.

It provides a physical basis for the proposed inflation of the early universe immediately after the Big Bang.

It provides [Part II, in preparation] an explanation for the nature and origin of dark matter within the same theoretical framework of compressible fluid flow as being a rarefied, energetic, gravitating substance related to and generated from ordinary matter.

It provides an explanation for the ‘dark energy’ postulated to explain the recently observed increased rate of cosmic expansion,.

It provides a unification of quantum physics and gravitational force.

The ability of a theory to provide a linked explanation for so many basic, disparate, physical phenomena from the single physical postulate of the reality of an energetic compressible fluid medium is obviously a strong argument in favour of its general validity and its being worth detailed theoretical examination and further experimental verification.

References and Notes

1. Turner, M. S., Quarks and the Cosmos. Science, 315, 59, 5 Jan. 2007.

2. Bergmann, Peter G. Introduction to the Theory of Relativity . Dover, New York. 1976.

3. McCrea, W. H., Cosmology. Reports on Progress in Physics. Pp 321-363, Vol XVI, 1953.

4. Chaplygin, S., Sci. Mem. Moscow Univ. Math.Phys. 21, 1 1904.

5. Shapiro, A. H. The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 vols. John Wiley and Sons, New York, 1953.

6. Bachall, N.A., Ostriker, J.P., Perlmutter, S., and P.J. Steinhardt. The Cosmic Triangle: Revealing the State of he Universe. Science, 284, 1481 1999.

7. Kamenshchick, A., Moschella, U., and V. Pasquier. An alternative to quintessence. Phys. Lett. B 511, 265, 2001.

8. Bilic, N., Tupper, G.B., and R.D. Violier. Unification of Dark Matter and Dark Energy: The Inhomogeneous Chaplygin Gas. Astrophysic , astro-ph/0111325. 2002.

9. Lamb, Horace., Hydrodynamics. Dover, New York, 6^th edition. 1932 .

10. Brennen, Christopher E., Cavitation and Bubble Dynamics. Oxford Univ. Press. 1995.

11. Frenkel, J. Kinetic Theory of Liquids. Dover, New York, 1955.

12. Kittell, Charles. Introduction to Solid State Physics. , 6^th. ed. John Wiley & Sons Inc., New York, 1968.

13. Courant, R. and Friedrichs, K. O. (1948). Supersonic Flow and Shock Waves. Interscience, New York,1948.

14. Power, Bernard A., Some of the work leading up to the present theory has appeared in connection with studies into the scientific basis for the image formation on the Holy Shroud of Turin. Some of these are as follows:

15. ---------------, Il Meccanismo di Formazione dell’Immagine dela Sindon di Torino, Collegamento pro Sindone, Mgggio-Giugno, pp13-28, 1997, Roma.

16.---------------, Caratterizzazione di una Lunghezza d’Onda per la Radiazione che Potrebe aver Creato I’Immagine Della Sindone di Torino. Collegamento pro Sindone, Roma. Novembre-Decembre, pp. 26-36, 1999.

17.---------------, An Unexpected Consequence of Radiation Theories of Image formation for the Shroud of Turin. Proc. Worldwide Congress Sindone 2000, Orvieto, Italy, Aug. 27-29, 2000.

18.---------------, Image Formation on the Holy Shroud of Turin by Attenuation of Radiation in Air. Collegamento pro Sindone website (www.shroud.it/) March 2002.

19.---------------, How Microwave Radiation Could Have Formed the Observed Images on The Holy Shroud of Turin. Collegamento [ro Sindone Website, Jan. 2003. (www.shroud.it/)--------------, Shock Waves in a Photon Gas. Contr. Paper No. 203, American Association for the Advancement of Science, Ann. Meeting, Toronto, Jan. 1981.

20.---------------. Unification of Forces and Particle Production at an Oblique Radiation Shock Front. Contr. Paper N0. 462. American Association for the Advancement of Science, Ann. Meeting, Washington, D.C., Jan 1982.

21.---------------, Baryon Mass-ratios and Degrees of Freedom in a Compressible Radiation Flow. Contr. Paper No. 505. American Association for the Advancement of Science, Annual Meeting, Detroit, May 1983.

22.---------------, Summary of a Universal Physics. Monograph (Private distribution) pp 92. Tempress, Dorval, Quebec, 1992.

23. ----------------,Appendix A ( below) Thermodynamic properties of an isothermal gas law for the Chaplygin/tangent field. 2006.

24. ---------------, Appendix B (below) A New Explanation for the Anomalous Weak Tensile Strengths of Liquids and Solids. 2006.

25.----------------, Appendix C (below) A Derivation of the Schrödinger Equation from the Concept of a Universal Wave Field. 2006.

26. ----------------, Appendix D (below) Philosophical and Theological Caveat. 2007.

27------------------, (a) www.shroudscience.info and open the page entitled Properties of a Universal Wave Field.

(b) www.energycompressibility.info

28. Guth, Alan. The Inflationary Universe. Jonathah Cape, London, 1997.

Copyright Bernard A. Power, April 2007

Appendix A

Thermodynamic properties of an isothermal gas law for the Chaplygin/tangent field

Bernard A. Power^a)

2006

An isothermal equation of state is formulated to match the adiabatic Chaplyin/tangent gas, and it appears to be a general gas law for a whole field whose thermodynamic properties are very unusual. In this field a working substance expands with cooling and contracts with heating, and both processes take place without any work being done. The 2^nd Law is inapplicable.

The theoretical or exotic fluid known as the Chaplygin/tangent gas has an adiabatic equation of state which has been widely studied and applied in aerodynamics and fluid dynamics for many years.^1,2,3,4,5,6 However, the adoption by cosmology of the negative pressure attribute of the Chaplygin gas as a possible solution to the observed increased expansion of the cosmos is only recent. ^7,8,9 A potential role as a universal cosmic fluid, however, would seem to merit an examination of all aspects of this field.

The equation of state for the Chaplygin gas is the linear relationship p = − Av, (pv^-1 = −A) ; it lies in Quadrant IV of the p-v diagram where it always has negative pressure. The dynamically identical Tangent gas has an added constant and is also linear, with p = − Av + B, ( pv^-1 = −A + B] ; in Quadrant I it has positive pressure (Fig. 1).

The Chaplygin/tangent gas can also be described by the adiabatic equation of state pv^k = −A, where A is a positive constant, k has the value of − 1, and where the minus sign preceding the constant A provides a desired negative slope –dp/dv on the pressure-volume diagram.

The proposed isothermal equation of state for this field is p = +Av corresponding to the adiabatic Chaplygin gas, and p = +Av –B corresponding to the adiabatic tangent gas. If the positive constant A is multiplied by a constant temperature T_c, we would then have p/v = A (T)_c , p = vAT_c, and p = vAT_c − B, which provide the desired isothermal relationship, provided that A takes on the proper dimensions. The isotherms in pressure and volume are seen to be strictly orthogonal to the adiabatics of the Chaplygin and Tangent gas. (Fig. 1)

Since v = 1/ρ , these linear isothermal relationships in pressure and volume ( p = vA T_c , etc ) can also be written hyperbolically in pressure and specific density ρ as

pρ = AT (1)

The ideal gas law ( pv = RT) is hyperbolic in pressure and volume, but linear in pressure and density ( p = ρRT). The proposed new isothermal equation of state for the k = −1 field is the reverse, being linear in pressure and volume and hyperbolic in pressure and specific density.

It would appear that the new relationship is not so much just an isothermal counterpart to the Chaplygin/tangent gas, but rather that it plays the more fundamental role of being the general gas law of the field, with the Chaplygin and tangent cases being simply the exceptional modifications to the gas law that apply under the adiabatic condition ( dQ = 0), just as is the case with real adiabatic gases which depart exceptionally from the ideal gas law. The term universal field ( UF) would embrace both the isothermal and adiabatic equations and where the “isothermal” equation we have derived would become the basic gas law ( pρ = AT )for the whole field.

The thermodynamic properties of this UF are very unusual because of (1) the direct proportionality of pressure and volume, (2 a negative specific heat either at constant volume or at constant pressure and (3) the positive slope +dp/dv of the isotherms on the pressure-volume diagram and its effect on expansion or contraction..

First, the isothermal pressure increase with volume expansion is the inverse of that for the ideal gas

Second the entropy relationships in the UF are also unusual since we have k = c_p/c_v = −1, so that either c_p or c_v must be negative. In the ideal gas with T and V as independent variables the entropy change is ∆S = c_v ln (T₂/T₁) + R ln(V₂/V₁). And with T and P as independent variables, it becomes ∆S = c_p ln (T₂/T₁) – R ln(P₂/P₁)

In the UF we have dS= c_v dT + (∂P∂T)_v and, from P =AvT we have (∂P∂T)_v = Av²/2 so that we obtain the corresponding entropy changes in the UF as ∆S = c_v ln (T₂/T₁) + Av²/2 and ∆S = c_p ln(T₁/ T₂) ) −Av²/2

(In the UF the magnitude of the reversible heat Q_r needed to calculate the entropy change ∆S is readily visualized on the pressure volume diagram, since the Carnot cycle is then depicted simply as the rectangle formed by the appropriate linear adiabatics and isothermals, and Q_r is the area enclosed).

Third, the positive slope +dp/dv of the isothermals on the pressure-volume diagram implies that there is no resistance to pressure/volume increases or decreases, which would therefore take place at ever increasing speed following any initial impulse.. This is analogous to an expansion into a vacuum in the usual analysis of an isothermal process in an ideal gas where the work pdV is then zero In the UF in an isothermal process it would seem that this work would also necessarily approach zero. This would mean complete reversibility of all UF processes, both adiabatic ( Chaplygin/tangent) and isothermal, with no preferred direction for any physical change. All complete cycles in the UF would appear to be isentropic. Heat would be convertible into internal energy but not into work.. The 2^nd law of thermodynamics would not apply. Clearly the properties of this unusual field should be further explored and critically evaluated.

References

1.. S. A. Chaplygin, “On Gas Jets,” Sci. Mem. Moscow Univ. Math. Phys. 21, 1 (1904).

2. H.S. Tsien, “Two-Dimensional Subsonic Flow of Compressible Fluids,” J. Aeron. Sci. 6, 399 (1939).

3. T. Von Karman, “Compressibility Effects in Aerodynamics,” J. Aeron. Sci. 8, 337 (1941).

4. A. H. Shapiro, The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 Vols.( John Wiley & Sons, New York, 1953).

5. R. Courant and K. O. Friedrichs, Supersonic Flow and Shock Waves. (Interscience , New York, 1948).

6. Horace Lamb, Hydrodynamics. 6^th ed . ( Dover Reprint, Dover Publications Inc. New York, 1936 ).

7. N.A. Bachall, J.P. Ostriker, S Perlmutter and P.J. Steinhardt. “The Cosmic triangle: Revealing the State of the Universe,” Science, 284, 1481 (1999).

8 A. Kamenshchick, U. Moschella and V. Pasquier, “An alternative to quintessence,” Phys Lett. B 511, 265 (2001).

9. N. Bilic, G.B. Tupper and R.D.Viollier, “Unification of Dark Matter and Dark Energy: The Inhomogeneous Chaplygin Gas,” Astrophysics, astro-ph/0111325 ( 2002).

Appendix B

A New Explanation For the Anomalous Weak Tensile Strengths of Liquids and Solids

Bernard A. Power

December, 2006

The observed tensile strengths of liquids and solids are orders of magnitude lower than the theoretical values. The discrepancy is explained by heterogeneous nucleation of the ruptures. However, the purely spherical expansion of rupture voids or bubbles may involve an adiabatic expansion of pv⁷ = const., giving much lower theoretical tensile strengths which are in agreement with the observations. The concept should be of interest to materials science.

Introduction

Theoretical estimates of the tensile strength of solids and liquids give values of around 3 x 10⁹ to 3 x 10¹⁰ N/m^2. ( 3 x 10⁴ to 3 x 10⁵ atm.). However, for solids the experimental values are around 100 times smaller, while for liquids, such as water, the observed values are even smaller at 50 to 200 atmospheres [1,2].

The simple Frenkel derivation [2,3] of the theoretical tensile strength of solids or liquids gives a fractional volumetric expansion ratio ∆V/Vo needed to cause rupture and form the bubble, and this then is equated to an average numerical value of about 1/3. Then, since liquids and solids have compressibility moduli K which are about 10¹⁰ to 10¹¹ kg/m² ( i.e. 10⁵ to 10⁶ atmospheres ), we have a rupture pressure p_max = −K(∆V/Vo). Taking the average 1/3 value for ∆V/Vo, the heoretical rupture pressure p_mac then is between 3 x 10⁴ and 3 x 10⁵ atmospheres

Curiously, however, the high theoretical values of tensile strength do match the observed critical temperature for rupture by boiling. Why then does the theory fail in the case of rupture by tension where the observed values are so low?

For solids, the discrepancy in tensile strength is usually ascribed to heterogeneous nucleation of rupture at defects such as cracks or dislocations in the lattice [1]. In the case of liquids, the even larger discrepancy is explained by invoking the presence of irremovable tiny gas or solid nuclei within the liquid which act to lower the pressures and tensions needed for mechanical rupture [3]. Still, there remain discrepancies, and the foreign nuclei explanation, or heterogeneous nucleation process, acting alone, have appeared somewhat artificial, especially since the thermal rupture (boiling) values do agree with the theory.

Recently it has been realized that a mechanism exists in the cavitation process which may act to greatly lower the tensile strength predictions of theory and to reconcile them with the observations.

The basic mechanical equilibrium equation for the production of a spherical void, or vapour- filled bubble, in a liquid by rupture is

p_B − p_L = ∆p_max = 2 σ /R_C (1)

which gives the relationship between the vapour pressure in the bubble p_B, the pressure in the surrounding bulk liquid p_L, the interfacial surface tension σ and the radius of the spherical bubble at the rupture radius R_C .

The formation of a bubble by rupture requires a negative pressure exceeding the tensile strength 2 σ/R in order to create the spherical void, R being typically the bond length in liquids, say around 2 x 10¹⁰ m. At this rupture radius, with σ having the value for water of around 10^-2 N/m ( 100 dynes/cm), ∆p_max has the value of 10⁸ kg/m² ( 10⁴ atm.).

Any incipient void in the liquid may fill with vapour molecules. In expansion this has little effect; in bubble collapse however, it is significant.

While liquid water has a value for k = c_p/c_v of around 1.1, it does not ordinarily have a well defined equation of state pv^k = const. However, Courant and Friedrichs [4] discuss the expansion and contraction of spherical blast waves in water and fit the experimental data to a quasi-equation of state for water under a pressure of around 3000 atm. which is pv⁷ = const or p =A ρ⁷ + B. They also derive the same value of k = 7 as a theoretically solution to their non-linear flow equations for spherical ( i.e. radial) shock expansions in fluids.

If we now apply k = 7 to purely radial ruptures and void or bubble initiation in water, the Frenkel derivation of tensile strength becomes

p _max = −K ((∆V /Vo)⁷ = −K(1/3)⁷ (2)

Using the rupture pressures above, we get the theoretical tensile strength of liquids such as water to be − 10⁴ x [1/3]⁷ = 45.7 atm. In addietion, −10⁵ x [1/3]⁷ = 457 atm, which is now in general agreement with the experimental values.

This result may be expressed in a more general form by noting that Equation 1 is derived on the assumption that the temperature of the liquid is constant [2,3]. In this case k has the value of unity and the relation between p and v is the isothermal one pv+¹ = constant. Equation 1 can then be rewritten as

∆p = const./ ∆V = 2 σ /R_C (2a)

But if the isothermal assumption is replaced by an adiabatic radial expansion with k = 7 we would have pv⁷ = const., and so

∆p = const./ (∆V)⁷ = 2 σ /R_C (2b)

Consequently for any given value of R_C the radial adiabatic volume change ∆V now enters to the seventh power, explaining the observed order of magnitude of rupture forces in the general theoretical context of an equation of state for the rupture process.

To sum up, we now have two cases, the current theoretical one for random kinetic volume expansions with pv = const. and the spherical ( i.e. radial) volume expansion, each with different initiating rupture pressures.

Case 1.

Random kinetic motion expansion:.

Equation of State is pv = const.

V = 4/3 π R³ ; R ≈ (V)^1/3 and p_max = 2σ /R ≈ 2σ/ (∆V)^1/3 , so that p_max is inversely proportional to (∆V)^1/3

Case 2.

Spherical ( radial) expansion:

Equaton of Sate is: pv⁷ = const.

R ≈ (V⁷)^1/3 ≈ V^2.333 p_max = 2σ /R ≈ 2σ/ (∆V⁷ )^1/3 ≈ 2σ/ (∆V)^2.333 and here p_max is inversely proportional to ^. (∆V)^2.333 .

Clearly, bond breaking in spherical expansion will be much more efficient than random kinetic or thermal expansion, since the increase in R will be large for smaller changes in pressure. This agrees with the experimental rupture pressure data above.

For example, for a volume fluctuation ratio +∆V of 5, Case 2 would give a radius increase of 5^2.333 = 42.5. Clearly, radial expansion is a very efficient bond breaking and rupture mechanism

The energy source of the purely radial or spherical expansion motions can be thermal waves, ultrasonic source waves , point source cosmic ray impact etc. etc.

For solids the rupture flow, because of structural and steric hindrance to radial orientation by an appropriate energy source, may be only quasi- radial, and a value of k between 4 and 6 might then be appropriate, giving tensile strengths higher than liquids but still well below the classical theoretical estimates.

The proposed model would still require simultaneous radial rupture over a sufficient number of adjacent bonds, and therefore the theory of rate analysis still applies. At the physical level the rupture can still, of course, be either homogeneous or heterogeneous, and all the various physical mechanism are still in play. In particular, the vibration cavitation process [3] is of interest, since it would supply an orderly negative pressure perturbation over a wide enough field to bring about effective simultaneous rupture under the radial flow assumption. It would appear that the new model should be of interest to materials science.

References:

1. Kittell, Charles. (1968) Introduction to Solid State Physics. , 6^th. ed. John Wiley & Sons Inc., New York.

2. Brennen, Christopher E., Cavitation and Bubble Dynamics. Oxford Univ. Press. 1995.

3. Frenkel, J. (1955). Kinetic Theory of Liquids. Dover, New York.

4. Courant, R. and Friedrichs, K. O. (1948). Supersonic Flow and Shock Waves. Interscience, New York.

Appendix C

Physical Derivation of the Schrödinger Equation of Quantum Mechanics from the Concept of a Universal Wave Field

Bernard A. Power^a)

July 2006

1. Introduction

2. Schrödinger’s Derivation

3. UF Derivation

4. New Insights

5. Analogies to classical mechanics

6. Conclusions

1. Introduction

The Schrödinger equation for the hydrogen atom is based on the classical wave equation in the form of the Helmholtz oscillator. But the classical wave equation holds exactly only for the special case of the theoretical, compressible field or fluid called the Chaplygin/Tangent gas.

The theoretical or exotic fluid known as the Chaplygin/Tangent gas has an isentropic/adiabatic equation of state which has been widely studied and applied in aerodynamics and fluid dynamics for many years [3-7]. Recently, because of negative pressure attribute of the Chaplygin gas it has been proposed by cosmologists as a possible solution to the observed increased expansion of the cosmos [1,2]. Such a potential role as a universal cosmic fluid, however, would now seem to merit an examination of this field in relation to the quantum mechanics, starting with the basic Schrödinger equation for the hydrogen atom..

2. The Schrödinger Equation for the Hydrogen atom

Schrödinger based his derivation on the assumption of the classical wave or exact equation which, for compressive waves and expressed in terms of the wave function ψ for amplitude, is [7],

Ѳ ψ = 1/c² ∂²ψ/∂t²/ [ 1 + Ñψ ]^{(k + 1)} (1)

or, for one dimensional motion in the x-direction

∂²ψ //∂x² = [(1/c²) ∂²ψ /∂t² ]/ [ 1 + ∂ ψ /∂x ] ^1+k (2)

This exact equation means that for material gases ( k > 0) compressive waves are always unstable and grow with time . For very small amplitude waves however, the term in the denominator involving ∂ ψ /∂x approximates to unity, and the equation simplifies to becomes the classical wave equation

Ѳ ψ = (1/c² )∂²ψ/∂t² (3)

which has the general solution

ψ = ψ₁₍x – ct) + ψ₂ ( x – ct) (4)

In the case of the UF, however we see that, since k = – 1, the exponent ( k + 1) in the denominator of Eqs. 1 and 2 becomes zero, thereby automatically reducing the equation to the simple classical wave equation, but without any of the approximation needed for real gases such as air.

The UF is therefore truly unique in that it automatically becomes exact for waves of any wave amplitude, large or small and is no longer limited to infinitesimal waves as is the case with real gases .The UF is therefore unique among gases it is the only field in which the Classical Wave Equation is strictly valid and which therefore can transmit stable waves, of either condensation or rarefaction, of any amplitude.

For periodic motions the classical wave equation assumes the form

Ѳ ψ + [4π²ν²/c²] ψ = 0 (5)

called the Helmholtz equation which applies to periodic motions such as for the simple harmonic oscillator or for sinusoidal oscillations.

Since c/ ν = λ we can express it also as

Ѳ ψ + [4π²ν²/ λ ²] ψ = 0 (6)

So far this is classical mechanics, but at this point Schrödinger introduced the de Broglie relationship

λ = h/mv (7)

which gives us the equation

Ѳ ψ + [4π²m² v ²/h²]ψ = 0 (8)

Next he expressed the kinetic energy ½ mv² as [E – V] to get

Ѳ ψ + [8π²m² /h²] [ E –mV]ψ = 0 (9)

which is the time-independent form of his famous equation.

We see that Schrödinger’s derivation is straightforward classical wave theory up to the point of his introduction of the de Broglie relationship λ = h/mv.

2. The Derivation of Schrödinger’s Equation from the theory of the Universal Field , including derivation of the de Broglie Relationship

If we now turn to the concept of the Universal Wave field, we see that the classical wave procedure obviously also fits right up to the same key point of the de Broglie insertion. In fact, since this is the unique field supporting the wave equation,in the UF it fits even better than with Schrödinger’s original derivation.

In addition, we now show that the de Broglie relationship, in UF theory, becomes a physical requirement and no longer an arbitrary step as before.

To see this, consider the kinetic energy equation for compressible fluid flow

c ² = c_o² – V²/n −2cV/n (10)

where c is the actual wave speed, c_o is the static wave speed, V is the relative flow velocity and n is the energy partition parameter related to the adiabatic exponent k as k = (n+2)/n. As in all compressible flow theory the mass m is taken as being unsteady and is not explicitly shown. In the case of the UF we have n = − 1 .

The term 2cV/n is the unsteady energy of accelerated and pulsed flows. It leads directly to the de Broglie relationship as follows

2/n cV= E = hν = (m) λν V, so per cycle of the pulse ( i.e. dividing through by ν) we have

h = mν λ = p λ (11)

From this new viewpoint the de Broglie relationship is just the energy per pulse cycle ( E/ν) of an accelerated or pulsed flow in the UF expressed in terms of momentum ( p = mV) and the pulse wavelength λ. Therefore, its introduction into the Helmholtz periodic or standing wave relationship becomes natural and necessary to complete the energy balance. All previous arbitrariness in the derivation of the Schrödinger equation thereby vanishes.

Again we can understand the derivation of de Broglie relationship from the UF theory by considering the velocity additions c + V and c – V. The corresponding energies for unit mass m are the squares of the velocity sums, namely m(c² + V² + 2cV) and m(c² –V² – 2cV) respectively. If we understand mc² as the energy of the UF, and mV² as twice the kinetic energy , then mcV becomes the pulse energy .

Finally, we can look at the velocity addition of a pulse and the corresponding interaction energy as

(c + dc)(V + dV) = cv + cdV + Vdc +dcdV

Clearly for small V relative to c all terms are negligible except for the cV term which we then take as being the non-relativistic interaction energy of the mass particle. We also point out that in the UF any flow speed V whatever results in a wave speed c greater than the static or “no-flow” wave speed c_o. On the other hand, in the UF, shock waves can never form, since, while the Mach 1 condition can be approached, it can never be reached.

The non-relativistic” character of the Schrödinger equation is also in accord with this derivation since, for small flow velocity V, the energy term (m)V² is negligible in comparison with the 2cV term where c is always large. Hence, for “non-relativistic” flows only the latter term ( expressed as the de Broglie relationship ) is needed. Also, with small relative velocity V, the departure of the local wave speed c from the maximum or static value c_o is very small and so c_o can be used.

We can see this from the flow kinetic energy equation

c ² = c_o ² – 1/n( V²/c_o²) – 2cV/n

The relativistic correction centres around the departure of c from the stagnation wave speed c_o, that is to say, the Schrödinger equation assumes implicitly that c = c_o, as do all special relativity theories. This will be small either for small V or for larger n. Therefore, for more complex assemblages or interactions of the UF with matter such as with the de Broglie pulse interaction, the departure becomes progressively smaller and the non-relativistic approximation becomes improved.

References

1] A. Kamenshchick, U. Moschella, and V.Pasquier, Phys. Lett. B 511 (2001) 265-268.

[2] N. A. Bachall, J.P. Ostriker, S. Perlmutter, P. J. Steinhatrdt, Science, 284 ( 1999) 1481

[3] S. Chaplygin, Sci. Mem. Moscow Univ. Math. Phys. 21 (1904) 1.

[4] H.-S. Tsien, J. Aeron. Sci. 6 (1939) 399.

[5] T.. von Karman, J. Aeron. Sci. 8 (1941) 337

[6] A. H. Shapiro, The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 Vols. John Wiley & Sons, New York, 1953

[7] Lamb, Horace, Hydrodynamics, Dover, New York ,6^th edition, 1932 .

APPENDIX D

Philosophical Caveat

Any theory of cosmology inevitably brings up matters of interest to philosophy and theology such as the origin and nature of the universe, creation, evolution, and so on. It may be useful, therefore, to state as clearly as possible what new scientific raw material this new cosmological theory may provide for these two associated fields of human interest and study. The three intellectual disciplines of science, philosophy and natural theology, while rationally related, are autonomous and have different legitimate aims and methods. Most scientists are not expert in philosophy or theology, nor do all philosophers and theologians always properly understand science and scientific theories. In some cases, on the part of science, this can be the unavoidable consequence of a technical language or of a compressed presentation of theory. Consequently, we add a few words to try and avoid some unnecessary potential misinterpretations which might arise in the present case.

First, the new theory’s basic postulate is one of physical realism. The UF is experimentally verifiable. It is not a purely theoretical or ideal construct.

Second, the theory is rational. The Greek philosophical principle of non-contradiction applies. That is to say, it must be self-consistent and open to experimental falsification or verification according to ever emerging experimental data. There can be no internal ambiguities or inherent contradictions here, such as are held to be possible in some philosophies. If the theory is shown to be self-contradictory or significantly at variance with the data, it falls. Even if it should become widely accepted, it will still be subject to adjustment, and revision, even radical revision, according to the data.

Third, the basic physical postulate is radically contingent. That is to say the initial postulate of the existence of a universal primordial cosmic compressible fluid entity does not contain within itself any compelling reason that explains its own existence. It is not self-evident that it must exist, or has always existed and so on. Its scientific justification lies in its power to explain the experimental data. In other words, we maintain that the UF is real, and that it can be verified experimentally, but we have no knowledge of why it exists at all.

This can perhaps be seen most succinctly in its equation of state pv^k = constant, where the constant has the physical dimensions of an energy. It can theoretically have any value, positive or negative; so we cannot on theoretical or on mathematical grounds exclude any value, including zero and infinity. This raises the philosophical question of why the constant has the actual value that it does. Why is it this value, and why not some other value, or even why is it not zero, nor why can’t it eventually become zero and then reappear, or not, or even become infinity? These questions, while very relevant, are not for science to consider; science takes the best observed value or estimate and proceeds to study how the compressible entity actually works or behaves. Therefore, this new scientific theory is apparently a philosophical statement that its basic postulate is radically contingent, with no self-contained reason for its existence. Its validity is based on its remarkable ability to resolve many important and basic scientific questions from a single scientific postulate of a compressible continuum, and to do so in significant conformity with the experimental data.

This radical contingency apparently raises a fundamental philosophical and theological matter, since radical contingency according to philosophers brings up the philosophical necessity of a creation or a beginning, and thus of a Creator. One self-styled “modern pagan philosopher”, Mortimer Adler, has drawn attention to this, and even labels the existence of such radical contingency as being ‘proof of a Creator’ at an acceptance level of ‘beyond reasonable doubt’ [29]. On an even broader basis, the assertion of the physical reality of the new cosmology would appear to meet Lonergan’s criterion [29] for what constitutes philosophical reality, namely something which can be ‘ intellectually grasped and reasonably affirmed’, with the same exnihilation consequences for philosophy. That is to say, the UF is real if it obeys the rational laws of compressible fluid flow and if its theoretical predictions are critically verifiable in the experimental data.

As an example of the difficulties that can arise out of an apparently minor alteration in a concept in one discipline, there is the definition of physical matter in the present theory. While the philosophical doctrine of materialism is no longer much in fashion since the advent of quantum physics, clearly it will be important in any new definition of matter, or in a new theory of its origin, to get things straight. Here, we have defined matter as a condensed energetic ‘form’ emerging from the UF, and originating in the compression of the UF immediately preceding the Big Bang. This makes physical matter a ‘form’ with compressed energy, and definitely a quantified or physical entity. Also, the ‘dark’ matter as described in the theory is just as physical as ordinary molecular matter, but it is of a different nature in that it appears to be a physical form with a rarefaction of its energy density. Again, the electromagnetic invisibility and tenuousness of the UF may thereby make it prone to misinterpretation by those imaginatively inclined who may be tempted to confuse it with “spirit”. Here, a distinction between matter and spirit by Lonergan [30] may be helpful. He maintains that the spiritual is what the material is not. For example, he points out that the material is always intrinsically quantified – the electron always has a definite mass and so on - , but the spiritual is not intrinsically quantified; the soul in a human may be quantified in that person in the sense that it is intimately joined to the human bodily mass, but the spiritual in humans is not intrinsically quantified and can exist with any particular bodily quantification, or after death with none. Our point here is that the dark matter explanation we have offered of a World B rarefaction of energy density is that of a purely physical and quantified reality just as is ordinary World A matter. The UF and its dark matter are not some kind of “spirit” category just because they are “invisible” or “rarefied” in energy density. They are physical. Matter in the theory is either a condensation or a rarefaction of intrinsically quantified physical energy. Spirit and matter may indeed have something in common, such as both being created, both being dynamic, and so on, but the one is not the condensation of, nor the rarefaction of the other. Matter, whether ordinary or dark, is intrinsically quantified and therefore physical.

Clearly the fundamental concept of energy needs to be treated with care in any passage from science to philosophy and vice versa. Millennia ago Anaximenes proposed, following Thales and Anaximander , that all creation is a manifestation of one essential basic substance, but then in an extraordinary insight he added that all the different physical manifestations of existence we observe are various condensations and rarefactions of this elemental substance. The element he chose was atmospheric air -- an excellent basis for meteorology but not for modern physics. It was however, a remarkably close miss, being apparently the first introduction into cosmology of the notion of material transformations resulting from compressibility.

And yet the concept of the UF introduced here, while describing a compressible, energetic or dynamic continuum or field, does not depict any imagined “sea of energy”. We have no scientific basis for that concept. Energy as we know it does not exist per se but only in various definite quantified forms, such as elementary particles, atoms, molecules, photon, quanta and so on. The nature of the UF is that which is to be described by or grasped from its physics of compressible fluid flow; it is not to be found in an imaginative extension or reinterpretation. The pitfalls attendant upon the introduction of imaginative constructs into science are dealt with in Lonergan’s Insight [30] where he calls them “extra- scientific categories”. Such “attempts to use images in the place of concepts or to seek the absolute in the physical sphere” [31] have crept into cosmology as far back as Newton himself when he introduced his absolute space and time as an explanation for the origin of the forces acting in his rotating water bucket experiment. In the present theory, the UF is not presented as being an absolute reference space, although motion relative to it is theoretically predicted and can be experimentally verified.

Finally, any scientific theory must be revisable as other more concise theories are formulated, and especially as new experimental data become available. Consequently, any extension of a theory to philosophy and natural theology will also be revisable.

To take one historical example of what can happen, Albert Einstein had a very clear grasp of the physical consequences of his theories. A reading of the literature on relativity shows, however, that it was almost immediately reinterpreted philosophically and ideologically in innumerable ways, such as, for example, in the assertion that science now had established the ‘relativity’ of everything, even of truth and objective reality itself. Einstein never sanctioned this nonsense, and his direct and vigorous approach to scientific truth and reality is evident in one of his later remarks where he was discussing the possibility that Prof. Dayton C. Miller’s exhaustive optical repetitions of the Michelson Morley experiment at Mount Wilson, which always yielded positive but puzzlingly small experimental data against relativity and in favor of a detection of uniform motion through space, might or might not be true. In 1950 Einstein simply said: “If Prof. Miller’s results are verified, my theory falls. That’s all”. He would probably not have been much disturbed at Miller’s results being verified and explained in various new ways such as their being a physical compressibility effect rather then a Lorentz invariance effect. He would undoubtedly, however, have critically evaluated the data.

The postulate of the existence of the UF as a universal, physical, compressible continuum will also probably bring up the question of whether it also constitutes a quintessence or plenum [28]. These questions are at the interface between science and philosophy and care needs to be taken to hold to the actual scientific properties postulated for the UF and not to uncritically extend them during philosophical examination of the theory.

28. Sciama, Denis, W., Mach’s Principle 1979-1979. Great Ideas 1978. 57-67, Encyl. Britannica, Inc. 1978.

29. Adler, Mortimer, How to Think about God: A Guide for the 20^th- Century Pagan. Macmillan , New York. 1980.

30. Lonergan, S.J., Bernard, Insight: A Study of Human Understanding. Philosophical Library Inc., New York, 1957.

31 Power, J.E., Henry More and Isaac Newton on Absolute Space: An Extra-scientific Category. J. History of Ideas. pp 289-296.Vol. XXXI, No. 2, April-June 1970.

Note: Part II of this monograph entitled Origins of Matter, Dark Matter and Dark Energy is under preparation and will be posted here when it

becomes available.

Copyright Bernard A. Power, April 2007

Back to Main Page