COSMOLOGY OF A BINARY UNIVERSE

Part II

The Evolution of Physical and Biological Complexity

( January 2008)

Preface: The remarkable ability of the Chaplygin/Tangent gas, seen as a universal field (UF), to unify the forces of physics and to offer an explanation for the observed accelerated expansion of the universe has prompted further exploration of its possible use in problems of cosmic and biological evolution.

In Part I, the evolution of the UF itself was explored before and after the Big Bang singularity. The unfolding of our atomic and molecular world of astronomy which originated at the Big Bang was left for this Part II. However, this area has two aspects, one is the expanding material cosmos of atoms and molecules since the Big Bang singularity in which it originated, and the other is the development of the order and complex variety within this material world, which we call evolution.

The expansion phase of the atomic and molecular cosmos over the first 9 billion years or so has, until recently, been dealt with in cosmology by the general theory of relativity, which has had its difficulties. These stem from the fact that general relativity (1) has as its basic equation a postulated geometrical space and time (x,y,z,t) field or continuum in which accelerations ( i.e. gravitational force) are the results of a geometrical curvature of the postulated continuum, (2) its dynamical equation of force is a differential equation with no unique solution, and (3) it has no equation of state to physically account for the expansion of the cosmos which it is used to describe.

The UF on the contrary is a compressible physical field, whose basic equation is an integral equation of state with a unique solution, and whose expansion is naturally explained. Its force equation likewise stems from an integral energy equation whose space gradients set up the forces, explains their existence in a physical, instead of a geometrical, way, and unifies them all for the first time.

The world of material molecules and atoms since the Big Bang can be envisaged as a quasi-compressible fluid of atoms and molecules with an equation of state relating pressure, specific volume and temperature. However, the observed cosmos with its galaxies, clusters and immense voids is certainly not a close approximation to an ideal expandable gas, so that this approach is a matter for experts who have a full range of the essential data at hand. Consequently, for now, instead of treating the cosmology of the post-Big Bang expansion, we shall turn to the development of physical order and complexity and to biological evolution.

Although progress in the formulation of a satisfactory theory of biological evolution has been punctuated by a series of radical revisions, the thesis that biological complexity has evolved appears to be well established.

Darwin’s original explanatory theory, that this evolution has occurred by a natural selection of chance biological variations passed from one generation to the next, suffered a check when Mendel’s laws of inheritance were re-discovered. Mendel’s obstacle was the fixed inheritance of genetic characteristics, which was further solidified with the discovery of the genes and their DNA/RNA mechanisms. After a considerable time, Darwinism was revived as neo-Darwinism when probabilistic laws of gene combination were introduced, and the proposed evolutionary mechanism became, in effect, gene emergence probability.

However, the basic physics or biophysics of the problem still remained fundamentally unresolved, because the emergence of complexity in nature, such as in the formation of genes, appears to be in opposition to the 2^nd law of thermodynamics. In spite of this problem, plausible, but essentially incomplete, theories of automatic emergence of physical complexity skirting the 2^nd law have been developed, extended to the emergence of the genes, and a near final solution to the problem of the evolutionary mechanism is now sometimes asserted to have been achieved.

Some serious attempts to reconcile the emergence of complexity with the obstacle of the 2^nd law have been made, but these have not won general acceptance. In practice, the 2nd law problem is often just set aside as only a detail, destined to inevitably be resolved in some manner yet unknown. Detailed analysis of the emergence of physical complexity and its connection with evolutionary biology has been undertaken, but these efforts have lacked any integration with the underlying orderly physical forces that are the dynamism of change. The present situation might, not too unkindly, be characterized as an optimistic expectation that all will eventually be well and that, notwithstanding the 2nd law, biological order will eventually somehow emerge from random physical disorder.

Now, in the last few years, the emergence of the concept of a universal wave and force field (UF), derived from the so-called Chaplygin/Tangent gas of aeronautics and gas dynamics, has introduced a new level of basic physical order. This approach has succeeded in unifying the fundamental forces of physics, and so reconciles gravitation, electromagnetism and quantum physics. Based on this standard dynamics and thermodynamics of a compressible fluid medium, orderly force fields pose a fundamental problem for the neo-Darwinian theoretical assertion of a purely probabilistic emergence of physical complexity. This source of basic order in both physics and biology, and its interaction with probability to produce the complex physical and biological reality evolving around us is the subject of this monograph.

Contents

1. Introduction

2. The Forces of Nature: A Universal Wave and Force Field (UF) Related to the Chaplygin/Tangent Gas -- a Universal Source of Physical Order

3. The Emergence of Physical and Chemical Complexity: A Critical Analysis of the Complexity Theory of Nicolis and Prigogine

4. A New Approach to the Emergence and Evolution of Biological Complexity in the Aqueous Environment of the Living Cell.

4.1 Introduction

4.2 The Living Cell: An Aqueous Medium

4.3 The Adiabatic Rupture of Cell Water and the Effect of this Entropy Change on Biochemical and Genetic Reaction Rates

4.4 Chemical Reactions in the Aqueous Environment of the Living Cell: An Entropy of Liquid Rupture

4.5 Entropy Increase, the 2^nd Law of Thermodynamics and Evolution.

5. Conclusions on Biological Complexity: Do Orderly Forces Acting on Random Kinetic Motions Result in the Emergence of Variety on a Probabilistic Time Scale?

References

1. Introduction: Early theories of biological evolution, such as those of Buffon, and Lamarck, stressed the obvious morphological and functional adaptation that organisms have to their environment and asserted the inheritability of acquired adaptations. The theory was descriptive and speculative, but provided no physical mechanism to bring about either the claimed adaptation or its inheritance.

Charles Darwin’s original theory of evolution stressed the role of chance variations in automatically fitting the organism to its environment, followed by the survival of the fittest, and the passing on of this random variation in fitness to the offspring. The theory was factually descriptive, and based on chance, but its simplicity was a better fit to the canon of parsimony than earlier theories.

Mendel’s experimentally-based genetics then emerged to assert the impossibility of inheriting anything other than the genetic endowment. Darwinian chance variations were not inheritable no matter how fit they were. With fixed genes, evolution could not take place.

Neo- Darwinism overcame the Mendelian obstacle by postulating the random or chance emergence of new genetic material, combined with the subsequent non-random probabilistic survival of the genetically most fit population or sub-population. Given a sufficiently large genome or pool of genetic potentialities, the probabilistic emergence of new species would be automatically assured. The theory is quantitative via probability theory once the necessary genome size is somehow generated. The physical origin of the large genome pool is not rigorously addressed; instead the automatic emergence of physical complexity is implied.

A serious attempt to explain the role of entropy and the 2^nd law of thermodynamics in biological systems, where it appears to act in opposition to its role in non-living systems, has been made by Brooks and Wiley [1]. These studies have not been widely adopted, but they go directly to the heart of the problem in the search for a physical theory of evolution.

Recent studies by the Prigogine et al. school [2] have endeavored to properly ground the emergence of physical complexity in physics and chemistry, by studying the automatic emergence of complexity from random physical and kinetic motions when the random physical system is thermally stressed or not at equilibrium. This approach properly addresses some of the physics, but fails to include the role of the basic physical forces involved – orderly, non-random forces of gravitation fields, orderly non-random inertial forces, orderly pressure field forces, etc, etc, Thus, its assertion that the desired complexity simply emerges automatically from random kinetic systems is invalid, since it leaves out the role of the basic, non-random, physical forces that also participate in bringing about the new complex order on the observed probabilistic time scale.

In this present study, we shall (1) examine the role of ordered physical forces arising from the UF in bringing about physical complexity, (2) examine the physics of the rupture of water -- the aqueous environment of the living cell in which all biological reactions and processes take place, (3) introduce a new entropy of rupture into cell reaction kinetics, which in turn appears to be reflected in the observed logarithmic time scale of evolutionary history, (4) and, in addition to the role of the 2nd law in evolution, we shall introduce the possibility of two additional entropy regimes or entropy orders arising in the Universal Field,

which appear related to the observed orderly and complex characteristics of plant and animal life.

2. The Forces of Nature : The Universal wave and force field (UF) which is related to the Chaplygin/Tangent Gas: a universal source of physical order, waves and forces

2.1. The Forces of Nature

2.2. A Universal Wave and Force Field (UF) Related to the Chaplygin gas and Tangent Gas

2.3. Wave Motion in the UF

2.4. The Universal Field (UF) and the Transmission of Transverse Electromagnetic Waves in Space

2.5. Maxwell’s Electromagnetic Waves and the UF

2.6. Gravitational Force and the UF

2.7 The Strong and Weak Nuclear Forces: Strong and Weak Shock Options.

2.8. Summary

2.1 The Forces of Nature: The four fundamental forces of nature are gravitation, electromagnetic force, and the strong and weak nuclear forces. Other subsidiary or related forces are the intermolecular chemical forces among molecules such as the van der Waals and London forces, the force of surface tension, pressure gradient force etc.

The general definition of force is the space gradient of energy, or

F = dE/dx ( in one dimension )

An equivalent formulation is the dynamic or Newtonian definition of force:

F =m (dv/dt) = ma (in terms of particle mass m and acceleration a)

In any compressible fluid the force is given by the Euler equation which, for 1-dimensional flow is

∂u/∂t + u ∂u/∂x + v ∂u/∂y +w ∂u/∂z = −(1/ρ) ∂p/∂x

where p is the pressure, ρ is the specific density and the term on the right hand side is called the pressure gradient force.

Until the emergence of the UF theory, the concept of force in physics has been compartmentalized. Electromagnetism and the nuclear forces are conceived of as involving some sort of “exchange of particles”. In the case of the electromagnetic force, the particle exchanged is the photon, for nuclear forces the particles are gluons or the Z particle, and so on. For gravity, a “graviton” force particle has been postulated but has never been experimentally detected. In short, attempts to unify the concept of force in physics have, until recently, essentially failed.

The energy gradient definition ( 1) requires a non-uniform region in a field of energy where the force develops and acts on any material particle at that point. The relevant point we make here is that a field of energy and its space gradients is an existing orderly physical element. The existing elements are not just the molecular and atomic particles, but also include this force field which acts jointly with them to produce a resulting complex motion. Complexity in such a system thus arises automatically from the physics, but not solely from random kinetic motions of particles; instead it arises from the interaction of the random kinetic motions of the particles and the action of the co-existing orderly force field.

The second or Newtonian definition of force is phenomenological. It accurately describes what happens but does not address the physical origin of the force. When the particle is not accelerating there is no force present, when it does accelerate the force emerges. Newton does not advance any hypothesis here to account for the full nature and origin of the inertial force that his equation so well describes, any more than he does with his gravitational force F=m₁m₂ G/r² which travels across the cosmos to tie all matter together in orderly cosmic motions.

In addition to the four fundamental forces there are other derivative, well understood forces of nature such as the intermolecular forces which hold molecules together, the pressure gradient force in gases (Euler Equation), the surface tension forces on surfaces of liquids, vapour pressure forces. These are all ordered physical realities. They are not probabilistic in the sense that they sometimes have one value and sometimes another and that only their mean value is of physical significance -- they are always orderly and determinate.

The attempt to unify the various forces in terms of a grand unification theory has occupied physics for generations. While its accomplishment eluded physicists, there was no disagreement on the existence of forces as residing in quantitatively understandable orderly physical fields. Consequently, any attempt to understand the obvious emergence of physical complexity should therefore take the orderly nature of forces into account and not just focus on the random kinetic aspects of the material world. The emergence of complexity or evolution is thus to be seen as a binary process of probabilistic kinetics plus order.

It has proved possible to unify the forces of nature by postulating a universal wave field (UF) encompassing the Chaplygin/ tangent gas and its unique wave properties. This universal wave field has emerged from cosmology, where the recent discovery of the acceleration in the rate of expansion of the universe has quickly led to the application of a compressible exotic or theoretical fluid called the Chaplygin gas as a universal cosmic energy field [3,4,5,6,7,8,9,10,11].

Subsequent analysis of this exotic cosmic fluid (especially in a version introduced by Tsien [4, 1939] and von Karman [5, 1941] called the ‘Tangent gas’ in aeronautics ) plus the recent formulation of an orthogonal, isothermal equation of state for the field has led to the concept of a Universal Wave field (UF) [ 12 -22} with its remarkable wave and force properties.

Since this UF entity is compressible, it will yield a force identical to the Euler force equation already mentioned.

2.2 A Universal Wave and Force Field(UF) Related to the Chaplygin gas and Tangent Gas

The UF has the following Equation of state relating the thermodynamic variables p,v, ρ, and T

pρ = ART + B ; p = −Av +B

i.e. an adiabatic equation of state- corresponding to the Chaplygin/ tangent gas equation

pv^k = pv^-1 = const. with k = c_p/c_v = − 1; n = 2/(k − 1)

and an isothermal equation of state ( which in the case of the UF is uniquely orthogonal to the adiabatic equation)

p = +Av – B

The UF’s highly unusual properties include (1) the unique ability among known fluids or gases to propagate stable waves of any strength, which also (2) uniquely obey the simple classical wave equation, (3) a unique ability to support transverse waves, which is something impossible for any other known or theoretical fluid, and which thus provides for the first time a physical basis for the existence of the electromagnetic field and of electromagnetic waves, and for the transfer of radiation through space at the speed of light, (4) the unique ability to carry purely attractive gravitational waves which transfer gravitational force through space, and finally, (5) a unique linear wave field that may also serves as the basis for the transfer of quantum information through space at quasi-instantaneous speeds ( 10²³ m/s). .

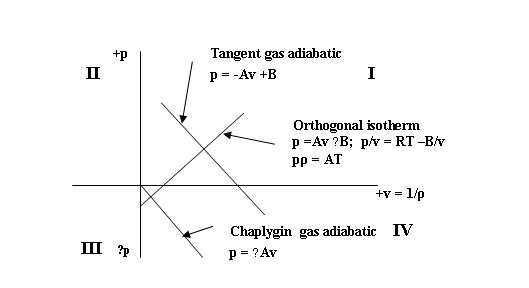
Fig. 1. Equations of State in the UF

2.3 Wave Motion in the UF

For simple compressive waves the exact wave equation [8], expressed in terms of the wave function ψ for amplitude, is

Ѳ ψ =( 1/c²) ∂²ψ/∂t² / [ 1 + Ñψ ]^{(k + 1)} (1 )

or, for one dimensional motion in the x-direction

∂²ψ //∂x² = (1/c²) ∂²ψ /∂t² / [ 1 + ∂ ψ /∂x ]^{(k +1)} (1a)

This exact equation means that for material gases ( k > 0) compressive waves are always unstable and grow with time. For very small amplitude waves, however, the term in the denominator of Eqs. 1 and 1a involving ∂ ψ /∂x is approximately unity, and the equation simplifies to becomes the classical wave equation [8]

Ѳ ψ = (1/c² )∂²ψ/∂t² (2)

which has the general linear solution

ψ = ψ₁₍x – ct) + ψ₂ ( x – ct) (2a)

In the case of the UF, however we see that, since k = – 1, the exponent ( k + 1) in the denominator of Eqs. 1 and 1a becomes zero, thereby automatically reducing them to the simple classical wave equation, but without the restriction to small amplitudes necessary for molecular gases such as air.

The UF is therefore truly unique in that it is automatically exact for waves of any wave amplitude, large or small and is not limited to infinitesimal waves as is the case with real gases. The UF is therefore unique among gases since it is the only field in which the Classical Wave Equation is strictly valid and which therefore can transmit stable waves, of either condensation or rarefaction, of any amplitude.

So far we have not distinguished between longitudinal and transverse wave motions in the UF. Clearly there is no problem with stable longitudinal waves; they are uniquely supported in the UF, and, moreover, they are not restricted to low amplitude acoustic type waves as in real gases where k is positive.

We shall now present evidence that transverse waves are also uniquely supported in the UF and that they in fact correspond to Maxwell’s electromagnetic waves.

2.4 The Universal Field (UF) and the Transmission of Transverse Electromagnetic Waves in Space

We should point out that this is an entirely new concept which emerged only in 2005 after an analysis of the isothermal properties of the exotic cosmic UF. It has been known for over a century that real gases can only support longitudinal waves, that is waves in which the density variations ±∆ρ are along the direction of wave propagation. Real gases cannot support transverse waves in which the density variations would be transverse to the direction of wave propagation. It was this inability to transmit the transverse waves of light which led to the demise of the old luminiferous ether concept. We now ask: What is the evidence for transverse fluid waves in the Universal Wave Field (UF ) with its orthogonal adiabatics and isotherms?

We consider a simple pressure pulse ( ±∆p) in the UF as in Fig.6 below:

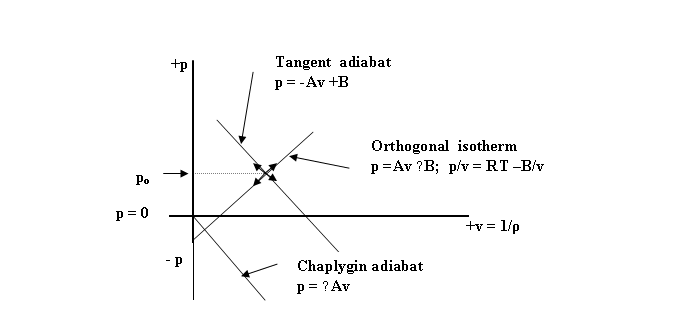
Figure 6. A pressure pulse ( ±∆p) in the Orthogonal Environment of the UF

The initial or static state is designated as p_o. When the pressure pulse ( +∆p) is imposed from outside in some way, the UF must respond thermodynamically in two completely orthogonal and hence two completely isolated ways, namely, by (1) an adiabatic stable wave along the adiabatic ( TG) and (2) by an isothermal stable pulse along the isotherm (OG).

Spatially, the pressure disturbance ( +∆p) must propagate in the direction of the initial impulse. But, since the two components of the pulse are orthogonal, they must still remain completely independent and physically isolated.

The only way possible for this to take place is for the two mutually orthogonal components to also be transverse to the direction of propagation of the two pressure pulses. Vectorially, this requires an axial wave vector V in the direction of propagation ( say z) with the two pulses orthogonally disposed in the x-y plane. i.e. TG X OG = V, which is evocative of the Poynting energy vector S = E x B in an electromagnetic wave.

E

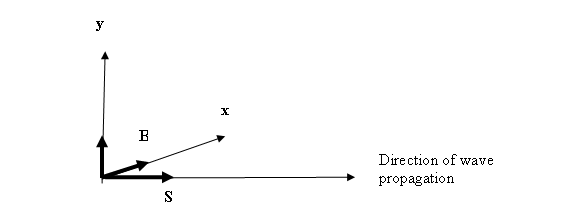
A wave of amplitude ψ traveling in one direction (say along the axis x) is represented by the unidirectional wave equation

dψ/dx = 1/c dψ/dt

2.5 Maxwell’s Transverse Electromagnetic Waves and the U.F.

Here, however, in the case of our adiabatic and isothermal pressure pulses, we have two coupled yet isolated unidirectional waves, and this reminds us of Maxwell’s coupled electromagnetic waves for E and B, as follows

dE_y/dx = (1/c) dB/dt and dB_y/dx = (1/c) dH/dt

where c is the speed of light, E is the Electric intensity and B is the coupled magnetic intensity.

Maxwell’s E and B vectors are also orthogonal to each another and transverse to the direction of positive energy propagation.

Therefore, we have established in outline an orthogonal two component wave system in the Universal Field (k = −1) which formally corresponds to the E and B, two component, orthogonal system of Maxwell for the propagation of electromagnetic waves through space in a continuous medium. His equations for E and B are

Curl E = ∂E_y/∂x = −(1/c) ∂B/∂t (3)

Curl B = ∂B_y/∂x = − (1/c) ∂E/∂t (3a)

If we now designate our Tangent gas as A ( for Adiabatic) and our Orthogonal gas as I ( for Isothermal) then our analogous wave equations would be

Curl A = ∂A_y/∂x = − (1/c) ∂I/∂t (4)

Curl I = ∂I_y/∂x = − (1/c) ∂A/∂t (4a)

The two systems are formally identical. Therefore, we propose that the medium in which Maxwell’s transverse electromagnetic waves travel through space is physically identified with a Universal Compressible Field (UF) having the above described thermodynamic properties for adiabatic and isothermal motions initiated in the UF by imposed pressure pulses ( presumably by accelerated motions of electric charges.) The compressibility property of the UF now properly accounts on physical grounds for the observed finite wave speed (speed of light c = 3x10⁸ m/s)); moreover, wave motions in this fluid medium are transverse as required by the electromagnetic observations.

It is possible to reduce Maxwell’s two equations UF equations to a symmetrical single wave equation

∂²E/∂x² = (1/c²) ∂²E/∂t² (5)

∂²B/∂x² = (1/c²) ∂²B/∂t² (5a)

and similarly with A and I for our Adiabatic/Isothermal coupled wave in the UF:

∂²A/∂x² = (1/c²) ∂²A/∂t² (6)

∂²I/∂x² = (1/c²) ∂²I/∂t² (6a)

This is not surprising since the UF, with its k = −1 thermodynamic property, is the only compressible fluid which automatically generates the classical wave equation ( Eqn. 2) with its stable, plane waves. The formal agreement of the UF theory with Maxwell is again striking.

Instead of taking our initial external perturbation as a pressure pulse ( +∆p) we should more realistically from the physical standpoint take it to be a density condensation (s = ( ρ – ρ_o ) / ρ_o = +∆ρ/ ρ_o). This will now result in a positive pressure pulse (+∆p) appearing in the adiabatic (TG) phase of the UF but a negative pressure pulse ( −∆p) in the isothermal or orthogonal perturbation component (OG) . This perturbation is represented by the two orthogonal sets of arrows on the pv diagram, one corresponding to +∆p and the other set corresponding to − ∆p. As the wave progresses the two orthogonal vectors also rotate.

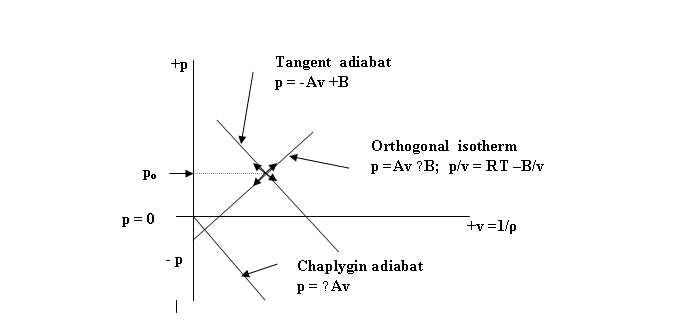
Figure 5. The physical ambiguity which results from a pressure/density perturbation in the Tangent/Orthogonal UF

An oscillating density perturbation ( ±∆ρ) then results in an axial wave vector having two mutually orthogonal components of a density perturbation wave. This appears to correspond formally to the Maxwell electromagnetic wave system with its two mutually orthogonal vectors for electric field intensity E and magnetic field intensity B.

We have thus established a case for the compressible UF being a cosmic reality which generates and transmits transverse electromagnetic waves through space.

These waves with their oscillating space gradient of energy ( i.e. of force) generate the electromagnetic force.

2.6 Gravitational Force and the UF

Here we shall not go into details, but the analysis of the UF waves also provides for the first time a system of exclusively attractive gravitational force as required by Newton’s force equation.

Briefly, in any compressible fluid, force is given by the Euler equation , which for 1-dimensional flow is

F = ∂u/∂t + u ∂u/∂x + v ∂u/∂y +w ∂u/∂z = −(1/ρ) ∂p/∂x

where the term on the right hand side is called the pressure gradient force.

In any compressible fluid medium, waves set up local transient pressure forces. Most waves in real gases and fluids are pressure oscillations (±∆p) and so they do not exert any net directional force on a material object they encounter. However, in the UF special types of waves can occur which can be either exclusively pressure compressions (+∆p) thereby exerting a net repulsive force on any material body in their path, or they can be exclusively pressure rarefactions (−∆p) which would then exert exclusively attractive force.

Consider Figure 6 where a condensation pressure pulse (+∆ρ; +∆ρ) imposed on the initial static pressure p_o in the UF will produce a rarefaction pressure pulse (−∆ρ) in the isothermal mode of response. Consequently, a source of pressure condensations will produce a train of isothermal pressure pulses as a response in the UF, and these pulse will travel spherically outwards through space.

When these rarefaction waves eventually impact a material body (mass) they will exert a net attractive force on it. This mechanism therefore in simple outline is formally equivalent to the force of gravity being produced by a rarefaction pressure gradient force.

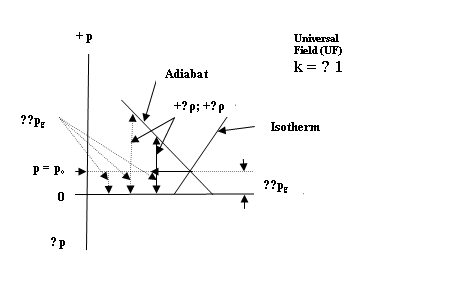
Figure 7. Positive density pulse ( +∆ρ) of any magnitude produces a quantized gravitational rarefaction pulse (−∆p_g ) of constant magnitude p_g =6.67 x 10^-11 kilopascals

2.7 Strong and Weak Nuclear Forces : Strong and Weak Obligue Shock Options.

We are not concerned with nuclear force in this monograph. However, for completeness, we note here that they also are explainable theoretically in compressible fluid flow theory via energy gradients which give rise to the forces ( F = dE/dx ).

There is another interesting compressible flow phenomena, that of shock discontinuities. In strong shocks, the energy gradient in the shock discontinuity is very large, and so the resulting associated force is also very large, and vice versa for the weak shock phenomenon. Furthermore, in oblique flow past an obstacle, the option may occur for either one or the other shock to occur. This is depicted in the so called “shock polar” which is a representation of these two options in a two-dimensional flow situation ( in velocity coordinates u and v):

Weak intersection W

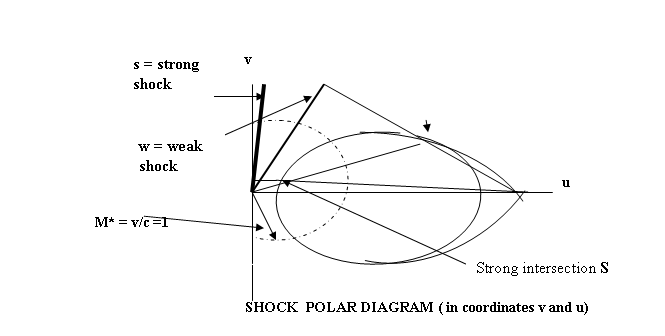
For each inlet Mach number M₁ ( = V_N1/c), and turning angle of the flow θ, there are two physical options:

1) the strong shock ( intersection S) with strong compression ratio and large flow velocity reduction (p₂ >> p₁; V₂ << V₁, and large spatial energy gradient and strong force (F_s = dE/dx ) , or

2) the weak shock (intersection W, with small pressure rise, small velocity reduction, small spastial energy gradient and weak force

Which of the two options occurs depends on the boundary conditions: low back, or downstream, pressure favours the weak shock occurrence; high downstream pressure favours the strong shock.

It is natural to consider whether these two shock options do not also correspond to the strong and weak nuclear forces. We point out, however, that the shock discontinuities in energy gradient ( dE/dx) which give rise to forces (F = dE/dx ) may actually have to reside in condensations of matter/energy and not in the UF itself. This is because in the UF the flow Mach number M = v/c may approach, but never reach or exceed unity, and therefore shock discontinuities or instabilities cannot occur in it; the UF supports only stable wave forms, although they may be of any strength, strong or weak The details of the nuclear forces do not concern us here.

2.8. Summary

Other minor forces exist, such as those of surface tension, intermolecular force and so on, but they are all variants of the fundamental forces set up by spatial energy gradients or by accelerations in the UF.

It may be worth restating here that this remarkable ability of the UF to unify all the forces of nature arises from its property that changes the sign of k in the equation of state pv ^k = const. from k = +1 ( ideal isothermal gas) to k = – 1 ( UF ). That gives us the UF orthogonal and tangent gas equations of state p = +A +B and p = −A +B, while the wave equation simply becomes the linear classical wave equation ∆² ψ = ( 1/c² ) d²ψ/dt^2. from which the forces emerge. All thus unification and simplification arising from a simple change of sign in the ratio of the specific heats k from positive to negative is truly astonishing.

This then completes our survey of the orderly wave and force field. We now return to the emergence of complexity in physical systems and then to applications to biological evolution.

3. The Emergence of Physical and Chemical Complexity. A critical analysis of the complexity examples of Nicolis and Prigogine

In their book Exploring Complexity, Nicolis and Prigogine [2] examine in detail the emergence of physical and chemical complexity from previously random kinetic systems such as gases and liquids when some source of additional energy is applied to the system in a non-equilibrium process which they term stressing of the system.

Various physical forces that are involved are mentioned, intermolecular forces and gravitation in particular, but they are treated by Nicolis and Prigogine simply as “givens” or adjuncts to the random kinetic motions of the atoms and molecules involved. This limited approach to the nature of the forces that cause the ordered motions and interactions leads to overlooking the orderly nature of the ever- present force fields that exist in each of the examples of complexity they present, and so to their faulty conclusion that biological complexity arises solely from random or kinetic physical events.

3.1. Their first physical example is the ‘ production of an ice crystal’ ( e.g. a dendritic snowflake ) from bulk water. They state that when the water is cooled below the freezing point the snowflake appears and grows. This, they argue is a simple example of the emergence of a highly ordered state from a disordered state, i. e. complexity emerges automatically upon cooling a liquid below its phase change temperature

Comment: Their first example is presented simply and makes no claim to exactness. However, we should point out that the process of snow flake production from water involves, not bulk water, but disordered water vapour. At most temperatures, the formation of crystalline ice from either bulk water or water vapour requires the presence of a suitable substrate or foreign ice nucleus whose preexisting orderly structure is essential to the initiation of the ice formation. Once nucleated, the type of crystal produced from water vapour is, moreover, not typically a dendrite, but depends instead upon the ambient temperature and pressure of the water vapour field surrounding the growing crystal. The crystal forms may range from needles to plates, to columns, to columns with plates attached to their ends, to dendrites and to other composite shapes depending on the ambient temperature and vapour pressure [24,25,26,27 ]. In addition, heat of sublimation is released in the change of state from vapour to solid ice and this evolved heat must be taken up by the total system as an entropy increase ( i.e a disorder increase). The vapour flows are governed by the vapour pressure gradient forces arising from the gas density gradients at the points where the water vapour interacts with the emerging crystal shape. The forces are not random and kinetic, but are orderly and determined by the gas law. Thus the resulting ice crystal shapes, once initiated by the pre-structured ice nuclei, are jointly determined by random or kinetic behaviour, by the orderly pressure gradient forces of an ideal gas, by the ambient temperature, and by the crystal energy requirements of the solid state that emerges. (Homogeneous ice nucleation can take place at around -40C but the argument is not essentially altered).

Clearly, the complexity which emerges upon ice crystal formation does not arise automatically from a purely kinetic state, but instead involves both a random kinetic component in the vapour and an orderly field of short range vapour pressure gradient forces around the growing ice crystal. (The force of gravity in this case acts only indirectly. But it should be remembered that it does produce the orderly ambient pressure field of the atmosphere, including its partial water vapour pressure component at the particular height above ground involved) .

Hence, in this case, complexity emerges, not automatically from kinetic disorder by self-organization as Nicolis and Prigogine concluded, but instead from an interaction of disorder and order. The orderly gravitational force produce an ideal gas field; the orderly vapor pressure gradients surrounding the random nucleating event produces an orderly snow crystal; the orderly crystal has a random element or sub-structure which manifests itself in a great variety of individual variations within the general crystal type dictated by the prevailing temperature and humidity of the vaporous environment ( 24,25 ].

3.2.’ Convection patterns in thermally disturbed fluids: Bénard cells’

This case is called by Nicolis and Prigogine “a prototype of self-organizational phenomena in physics” and so it will bear our careful analysis.

They discuss a shallow layer of water between two extended top and bottom plates. Left to itself the water rapidly assumes an equilibrium state of uniform temperature or uniform internal kinetic molecular disorder. If the system is now heated from below by a small amount, the injected heat is transferred upward by thermal diffusion, that is by the kinetic molecular motions under the action of the physics of a diffusion wave. Next, when more strongly heated by a certain critical amount, the temperature stress ∆T from bottom to top will set up a regular pattern of convection (Bénard) cells consisting of rising and descending fluid streams which organize into rotating cells. The direction of rotation seems to be random. This complexity or pattern has thus emerged automatically when the uniform state is stressed thermally and an energy flow is set up. The rising and falling motions are the result of density (buoyancy) differences in the various parcels of water, i.e. from assemblages of molecules large compared with the size of the individual molecules which are still undergoing only random motions. The fluid motions arise from the instability of dense and less dense water parcels side by side at a given level resulting in a descent of the more dense and the rise of the hotter ( less dense) parcels.

Various patterns of convection cells result depending on the boundary conditions and the vertical gradient of teméperature stress. For a sufficiently large heating, turbulent or disordered motions on the macroscopic scale set in.

This type of convective motion is treated in detail in texts on dynamical meteorology under the topics of potential instability and cumulus dynamics, where the density differences of perturbed air parcels under a uniform gravitational force field, combined with differential wind shear variation with height, explain the resulting cloud patterns and motions.

Nicolis and Prigogine conclude from their analysis that:

“ To summarize, we have seen that non-equilibrium ( heating) has enabled the system to avoid the thermal disorder and to transform part of the energy communicated from the environment into an ordered behavior. We can therefore cay that we have witnessed the birth of complexity. Our complexity achieved is rather modest, nevertheless, it presents characteristics that usually have been ascribed exclusively to biological systems. More important, far from challenging the laws of physics, complexity appears as an inevitable consequence of these laws when suitable conditions are fulfilled.”

Since the direction of rotation in the cells can be right handed or left handed and is apparently random, they also introduce the notion of chance at this point and draw a comparison between this and the randomness or chance asserted to exist in biological evolution where mutation is asserted by them to be controlled by chance and natural selection operates. No physical mechanism for this connection between physics and biology is offered.

On thermal convection phenomena they postulate (1) an initial uniform , kinetically disordered layer of fluid, plus (2) a thermal stress imposed on a boundary which sets up a gravitationally unstable stratification, and then at some critical value this results in ordered convection cells forming; this they interpret as being the automatic emergence of physical complexity from disorder.

Comment: We have several physical elements here: (1) a compressible fluid initially uniform and then (2) stressed or disturbed thermally to bring about an unstable stratification when (3) a suitable gravitational field also exists. Nicolis and Prigogine miss the importance of the presence and strength of the gravitational field. It is crucial to the emergence of the particular convection they cite. For example, if the gravitational field is absent, say in a space ship in outer space, no potential motion can exist and no cells can form. Again if the field is too weak, the cells can never reach the critical stress value. Again if the field is not uniformly vertical , but is converging or diverging, an entirely different complexity pattern and motion emerges. This specifically orderly gravitational field element is central to the existence and nature of the convection cell phenomenon, The phenomenon is therefore the physical result of the interplay of random kinetic molecular motions, ordered by gravity into an orderly pressure field (pressure of the fluid) plus the introduction of an asymmetrical temperature pulse, plus the action of an orderly gravitational buoyancy force field. The resulting complex behaviour then emerges, not from chance as they assert , but from the interplay of random or chance, probability laws, induced asymmetry and an ordered force field.

Thus, the Benard and convection cell phenomenon in their example is not one of emergence of complexity and order from physical randomness alone; instead, it is a complex physical interaction of factors, a stressed physical disorder plus an orderly physical force field. Physical complexity does not arise solely from disorder but from an interaction of disorder and imposed order. The Nicolis and Prigogine “prototype of self organization phenomena in physics” example is fundamentally flawed and incomplete as a foundation for their emergence of physical complexity thesis.

(Properly formulated, however, the Bénard cell example does show central features of the emergence of physical complexity in the physical world. Thus, they have chosen the proper example, even although it does not support their conclusions) .

3. ‘Self Organization Phenomena in Chemistry: The Belousov-Zhabotinski (BZ) Reaction’

Nicolis and Prigogine consider the state of equilibrium of any chemical reaction reached when two reactants produce a third chemical substance, or more typically two more substances

A + B → C + D and the reverse reaction

C + D → A + B

They then point out that, when certain of these reactions are disturbed or suddenly moved far from equilibrium, quite unexpected results are obtained

They then cite the BZ ( Belousov- Zhabotinski) reaction. For example, a solution of cerium sulfite Ce₂SO₄, malonic acid CH₂(COOH)₂ and potassium bromate KBrO₃ , in sulfuric acid, with an excess of Ce⁴⁺ ions gives a pale yellow colour, while an excess of Ce³⁺m ions gives no colour at all.

If now the reaction is carried out with stirring, several quite different types of behaviour are observed, namely oscillatory or clock-like behaviour of alternate colour and absence of colour, and chaos or turbulence.

If the reaction is carried out without stirring, orderly propagating wave fronts bring about the formation of spatial coloured spirals and spatial target patterns.

They then cite this behaviour as exemplifying the emergence of complexity from purely random or chance motions.

Comment

In their analysis of the B-Z chemical reaction Nicolis and Prigogine fail to discuss the actual forces involved. In chemical combination processes such as chemical reactions the relevant forces are intermolecular. These are Van der Waals forces arising from chemical dipoles existing in the asymmetrical atoms and molecules. It is these intermolecular forces which act to hold the various reacting chemical species or molecules together to form new chemical reaction products once they succeed in colliding with sufficient energy and entropy of activation. Without these forces of attraction, the molecules would simply collide and rebound kinetically and randomly as in a gas or liquid without combining at all.

However we have shown that all forces are orderly and arise from ordered deterministic force (linear and non-linear) and so their thesis that complexity is the automatic emergence of order, and pattern from random or chance subsystems alone is incorrect.

[Note. Later in Section 4.3 we discuss the entropy change in liquid ruptures that occur during reactions in solution and which are intimately connected with chemical reaction kinetics. They arise from ordered forces in a compressible medium, and have a key role in determining the rates of the chemical reactions; they are not described here as they are not essential to the present example].

3.4.’ Surface Tension Induced Phenomena in Materials Science’

Here they mention interfacial phenomena such as droplet formation and interfacial flows as examples of complexity emerging spontaneously from physical uniformity, but give no analysis and do not discuss the force of surface tension which again is ordered and not random..

3,5. ‘Cooperative phenomena induced by electromagnetic fields: electrical circuits, lasers, optical bi-stability’

The example offered here is the action of a coherent electromagnetic field ( a laser beam) injected into a resonant cavity filled with a suitable light absorbing medium. Under certain conditions the behaviour becomes bistable and can act as on optical switch. The behaviour is complex and non linear.

Comment: While the behaviour is complex, it is not the result of any spontaneous emergence of complexity from a non-complex or random predecessor state. Rather it is the result of a random (uniform) medium being acted upon by a highly-ordered electromagnetic field force.

The motions and forces in the e/m field are highly ordered. They are given by the Maxwell electromagnetic wave equations

Curl E = ∂E_y/∂x = −(1/c) ∂B/∂t

Curl B = ∂B_y/∂x = − (1/c) ∂E/∂t

Consequently, complexity arising in these systems must also reflect these highly ordered waves and their forces. It can still properly be called self-organization, because it is an entirely physical process, but it is not a chance mechanism. As we have seen in Section 2, the electromagnetic force arises from the occurrence of transverse waves in the UF, the fundamental field of physical order.

3.6. ‘Complexity in Biological Systems’

Here they state, “ Being convinced by now that ordinary physico-chemical systems can show complex behaviour presenting many of the characteristics usually ascribed to life …” They then describe in very general terms a few examples of biological systems.

This appears to be a greatly simplified claim. It might be more accurate to say “presenting some of the most elementary complex characteristics of living systems.”

Of course since biological systems undergo the same physical and chemical processes as do non-living systems, it is only natural to suspect that they also exhibit the same rudimentary complex characteristics that arise in non-living systems. The problem is not that biological systems are not as physical as non-living systems, but that they are so outwardly different from physical systems, and that we cannot presently explain why this is so in the necessary detail. In particular, so far as entropy flow is concerned, biological systems appear to violate the 2^nd law.

3.7. ‘Complexity at the Planetary and Cosmic Scale’

This is an interesting listing of complexity of physical events but the discussion is never at the level of the physical processes that occur. While it is open to an analysis that would include the details of the forces involved, it is not essential for our purposes and is set aside for some possible future exploration.

3.8. ‘The mathematical theory of complexity’. The bulk of the Nicolis and Prigogine analysis goes on to deal in some depth, with the mathematical theory of complexity, chaos and randomness. This will be very useful once the necessary clarification of the role of orderly forces that we are recommending is completed, so as to provide a formulation of a more complete theory of complexity, both physical and biological.

3.9 Conclusions on Physical Complexity

The general process under study is the action of fields of force on material particles (atoms and molecules) and on material assemblages of matter (gases, liquids and solids). In the absence of external force fields, the particles undergo random or purely kinetic motions. When orderly field forces are present they interact with the kinetic field and a composite pattern of order or complexity then emerges from the random chaos. It is our thesis that this binary, composite character of complexity must be considered in any account of the evolution of the physical universe and the biological world.

It should perhaps be noted in addition, that, with all physical force apparently arising from as universal field UF, this same field is uniquely orderly: (1) It is the only wave field that obeys the linear classical wave equation; (2) it alone supports and transfers stable waves of any amplitude; (3) it alone supports waves of both compression and rarefaction; (4) it alone accounts for the forces of nature and uniquely unifies them; (5) it alone supports transverse electromagnetic waves in space. Those unfamiliar with gas dynamics, acoustics and compressible flow may not fully realize how astonishing this all really is, but in fact, apart from the UF ( i.e. the Chaplygin/Tangent gas) in the physical world no kinetic molecular gas or compressible fluid can support stable linear waves of any finite amplitude whatever. All gases or compressible fields other than the UF are non-linear, unstable and tend towards shock discontinuities. If then, a unique orderly, stable, linear UF wave and force field underlies all the molecular physical world, and is the source of all its forces, then the proposition that complexity arises automatically and solely from molecular disorder and stress energy is untenable.

Many other physical interactions of force and kinetic interaction are of interest and remain to be studied. In the meantime we turn to biological complexity.

4. A New Approach to the Emergence and Evolution of Biological Complexity in the Aqueous Environment of the Living Cell Involving an Entropy Rate Factor 7^N

4.1 Introduction Up to this point, we have argued that complexity in the physical world results from an interplay of two elements, namely, random or kinetic elements on the one hand, and orderly forces on the other. Complexity is thus a binary physical process. In the following approach to explaining complexity in the biological world of living organisms, we shall cite these same two physical elements and their interaction as agents in bringing about the observed complexity.

We examine biological processes and evolution within the basic living cell. We concentrate on the physical forces that must be present to operate the metabolism of the living cell, to operate on the proteins and genes in the body cells so as to enable cell growth, the transmission of the organizing instructions to the cell component parts, and to operate on and occasionally to mutate or change the genes so as to transmit the biological integral forms from one generation to the next while still allowing for emergent change or evolution..

Clearly this approach is different from that of neo-Darwinian population genetics, which offers little on the physical processes underlying the emergence of the gene forms themselves and focuses mainly on the results of various probabilistic combinations within the given, already existing, very large gene pool. Physical process involved in conformational protein alteration and gene mutation, while involving probabilistic process, cannot be essentially or exclusively random since they involve orderly forces.

Our new physical approach also involves a closer look at the aqueous environment of the living cell. We look at biological interactions and reactions as taking place in an aqueous medium, that is, as chemical reactions occurring in suspension or in solution in the cell aqueous medium.

We shall first look at a neglected necessary physical step in any reaction in water, namely the local rupture and removal of the water films between reactant molecules in the living cell so that any collision between molecules can come to completion and allow the reaction to proceed. This new element of cell water rupture is then included in the energy of activation in standard collision theory of chemical reaction kinetics, or in the entropy of activation in the statistical mechanics approach to chemical reaction kinetics.[28].

4.2. The Living Cell: An Aqueous Medium

The living cell is typically quasi-spherical in shape and from 10 to 30 micrometers ( 10^-5 to 3 x 10^-5 m) in diameter. The cell is surrounded by a cell wall or semi-permeable membrane of lipids about 90 angstroms thick, which serves to isolate the cell from its environment so as to maintain its identity or homoeostatic nature. The cell membrane is reminiscent of the physical prototype of a lipid envelope in water- oil emulsions, or of the monomolecular films of various terpeneoid and essential oils from vegetation that coat atmospheric cloud droplets in most areas of the world.

The aqueous cell medium. The typical living cell is essentially a water globule, surrounded by a semi-permeable cell wall or membrane, and having in solution or suspension various organic structures, and with a central core of genetic material which directs the cell life, growth and reproduction. The essentials of life therefore take place in water, so that we must consider the physical properties of water in any biological process or function; it is not simply an inert physical medium.

Furthermore, at the basic physical level, any reaction or interaction in a liquid must involve the usual elements of (1) collision energy of activation ∆E and (2) the entropy of activation ∆S , both of which quantities are standard in chemical reaction theory [28]. It is suggested here that this entropy of activation also must include the energy involved in the rupture of the water film around or between the various suspended or dissolved chemical reaction species. That is to say, any liquid film that separates two reactant molecules must first be ruptured and removed before actual collision and subsequent reaction can occur. Only after this rupture has taken place and a ‘void’ has opened up can the chemical /molecular constituents collide, interact or reassemble.

The cell must obey the thermodynamics of the physical fields it encloses, in particular this means for biology that the entropy changes in the cell and in particular the direction of such changes must be considered. These may conveniently be summarized on the usual pressure volume diagram of thermodynamics as follows:

(1). Micell or Lipid-covered Water Droplet ( A Physical Analogue of the Living Cell



Properties

Simple ‘cell’ wall

Aqueous with random mineral species in solution

No fixed size. Size is determined by relative humidity of ambient vapour and surface tension

Minimum interior complexity

Non-living, non-reproducing, i.e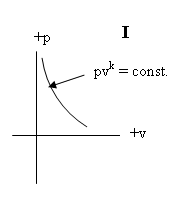. a simple kinetic physical system

Equation of state has form pv^k = const. (Quadrant I )

Internal de Broglie waves in aqueous fluid

Pressure, specific volume, density, temperature and pressure energy are all positive

Entropy change dS = dQ/T is always positive and the 2^nd Law of Thermodynamics holds

This order of entropy change( i.e. the 2^nd Law of thermodynamics) governs gas dynamics as it impacts on cosmic evolution

(2) Animal (plant) Cell

Properties

Complex cell wall

Aqueous with complex inclusions (Nucleus, orgnelles,

DNA/RNA etc)

Cell size 20-30 micrometers

Great interior complexity

Living and reproducing

Supports enclosed UF_I standing wave forms in Tangent gas and Orthogonal (isothermal) gas

Eqn. of state: Tangent gas p = −Av +B (Quadrant I)

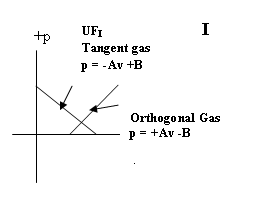Eqn. of state: Isothermal (Orthogonal) gas p = +Av −B

Entropy change in the Tangent gas, ds = dQ/T is positive, and 2^nd Law holds( i.e. “uniform disorder seeking”)

Entropy change in the Isothermal (Orthogonal) gas is zero, ds = 0/T = 0, ( i.e. “ stability seeking” )

Pressure positive (+p)

Specific volume positive (+v)

Specific density positive (+ρ) ( i.e.Wave forms are compressive)

Pressure energy is positive ( +pv)

It appears that the entropy change laws in Quadrant I of the p-v thermodynamic diagram would then enter into the nature and direction of plant and animal evolution as follows:

Quadrant I: (a) Tangent Gas: dS = dQ/T is positive ( 2^nd law of thermodynamics holds ( “disorder seeking”)

(b) Orthogonal ( Isothermal) Gas: dS = dQ/T = 0 ( “stability seeking” )

Note: There is another entropy condition in the UF , namely that in Quadrant II dS = − dQ/T, which has very unusual properties apparently matching the human condition. This is discussed briefly in Section 5 below, and in detail in Science and the Soul/Body Problem: An Exploratory Reassessment.

4.3 The Adiabatic Rupture of Cell Water and the Effect of this Entropy Change on the Rate of Biochemical and Genetic Reactions

The process of the formation of microscopic voids or micro- bubbles in a fluid which may lead to its rupture has been intensively studied in the phenomenon of cavitation and bubble formation, and in the reverse process of the homogeneous and heterogeneous nucleation of condensation of liquid from the vapour [28].

However, with respect to liquid rupture, we must take note of the fact that there is a long-standing major discrepancy between the theoretical and the experimentally observed tensile strengths for all liquids, and especially for the case of water. Recent work has offered a possible solution to this long standing problem by postulating an adiabatic rupture process instead of the usual isothermal one; this new approach has succeeded in a reconciliation of theory with observation. The new theory is as follows:

---------------------------------------------------------------------------------------------------------------------------------------------------------------

Adiabatic rupture as an explanation for the anomalous weak tensile strengths of liquids and solids

Bernard A. Power

Reviewed Aug. ^_ Sept. 2007: Revised Oct. 2007

The observed tensile strengths of liquids and solids are orders of magnitude lower than the theoretical isothermal rupture values. The discrepancy is currently explained by heterogeneous nucleation of the ruptures in the theory of nucleation rates. Still, the observations for water do not agree with current theory. However, an adiabatic rupture producing of voids or bubbles ( Equation of state pv^k = const.) would give much lower theoretical tensile strengths in agreement with the observations.. The concept should be of interest to materials science, to chemical reaction kinetics in aqueous solution, and so to cell biology and genetics.

________________________________________________________________________

1. Introduction

Theoretical estimates of the tensile strength of solids and liquids give values of around 3 x 10⁴ to 3 x 10⁵ atm.. However, for solids, the experimental values are around 100 times smaller than that, while for liquids, the observed values are 600 to 1500 times smaller at 50 to 200 atmospheres (Kittell, 1968; Brennan ,1995), with water being among the very lowest.

A simple classical derivation (Frenkel, 1955; Brennan 1995) of the theoretical tensile strengths of solids or liquids considers the fractional volumetric expansion ratio ∆V/Vo needed to form the rupturing void, and this then is equated to an average numerical value of about 1/3 . Then, since liquids and solids have compressibility moduli K which are about. 10⁵ to 10⁶ atmospheres, we have a rupture pressure p(max) = −K(∆V/Vo). Taking the average 1/3 value for ∆V/Vo , the rupture pressure p(max) then becomes the theoretical 3 x 10⁴ and 3 x 10⁵ atmospheres just mentioned, far higher than actually observed.

For solids, the discrepancy in tensile strength is usually ascribed to heterogeneous nucleation of rupture at defects such as cracks or dislocations in the lattice (Kittell, 1968). In the case of liquids, the even larger discrepancy is usually explained by invoking the presence of irremovable tiny gas or solid nuclei within the liquid, which act to lower the pressures and tensions needed for mechanical rupture. Still, there remain discrepancies, and the foreign nuclei explanation, or heterogeneous nucleation process acting alone, has appeared somewhat artificial, especially since the thermal rupture ( boiling) values do agree more with the theory.

2. Adiabatic cavitation

The basic mechanical equilibrium equation for the production of a spherical void, or vapour-filled bubble, in a liquid by rupture is usually expressed as a balance of forces inside and outside the spherical incipient void :

p_B − p_L = ∆p_max = 2 σ /R_C (1)

which gives the relationship between the (negative) rupture pressure ∆p(max), the interfacial surface tension σ, and the rupture radius r. This process is also assumed to take place at the temperature of the bulk liquid, that is to say isothermally.

The formation of a bubble by rupture thus requires a negative pressure ∆p(max) exceeding the tensile strength 2 σ/r in order to create the spherical void. However, instead of the isothermal process ( with general form of its equation of state pv⁺¹ = const.) which gives those unobserved high tensile strengths and rupture predictions, we could conceivably have an adiabatic rupture with pv^k = const. A, where k > 1. With k greater than unity, the adiabatic rupture pressure ∆p(max., adiabatic) will always be less than the presently assumed isothermal rupture pressure.

To see this more clearly consider the following:

The isothernmal bulk modulus or modulus of elasticity for a liquid K is given by

K_is = − v ∂p/∂v

And the adiabatic modulus is

K_ad = − v ∂p/∂v= k p where k is the adiabatic exponent or ratio of specific heats c_p /c_v

For liquids ( e.g. water )the two moduli have nearly the same numerical value.

The pressure at the critical point is then

p_(max.) = −K_is (∆V/Vo) and

p_(mac.) = − K_ad. (∆V/Vo)

The adiabatic bulk modulus K_ad. for water has the value 2.2 x 10⁴ atms. Table 1 then shows the effect of taking the adiabatic rupture/cavitation mechanism in water over a range of values of (∆V/Vo) i.e. (ρ/ ∆ ρ ) and for various values of the adiabatic exponent k from >1 to 7.. We point out first that V is the reciprocal of the density ρ, and so we can put _. (∆V/Vo)^{k =} (ρ/ ∆ ρ)^k which is more convenient., that is

P_(max.) = − K_ad. (∆V/Vo)^k = − K_ad(ρ/ ∆ ρ)^k

₍

The first step is the conversion of the liquid water in a small volume V to a “gas-like” structure at the critical point, which means a fractional volume expansion of about 0.333 (i.e. the density of water at the critical point drops from 1 to about 0.3333). This initial step obviously requires the injection of a sufficient energy. The rupture pressure in the new gas-like volume at this critical stage is now p_(mac.) = − K_ad. (∆V/Vo) = 2.2 x 10⁴ (0.333) = 7326 atm.

The second step is the adiabatic expansion of the same ‘gas-like’ volume to a larger bubble volume with consequent decrease of the pressure. Clearly, for any given expansion ratio, the adiabatic expansion yields a much smaller final rupture pressure than the usual isothermal rupture model. For example, in Table 1, a volume expansion of 1/3 (density ratio ρ/ ∆ ρ of 0.333) yields an isothermal rupture pressure of 7326 atmospheres, while the adiabatic expansion at k = 7 has a rupture pressure of only 10.1 atmospheres .(The experimental data also show a definite effect of temperature on the final rupture pressure; this does not affect the conclusions reached here, since they are based on comparative values of the isothermal and adiabatic processes at any given initial temperature).

Table 1

Adiabatic rupture pressure p _{( max.)} for water ( K_ad. = 2.2x10⁴ ) for various assumed values of density change ratio (ρ/ ∆ ρ)

Rupture pressure (p _{( max.)} ( p = K_Ad. (ρ/ ∆ ρ)^k)

(Atmospheres).

Density

Ratio

(ρ/ ∆ ρ)

k = 1** k = 2 k = 3 k = 4 k = 5 k = 6 k = 7

0.1 3300 atms. 220 22 2.2 0.22 0.022 2.2x10^-3

0.20 4400 880 176 35.2 7.04 1.41 0.28

0.30 6600 1980 594 178 53.5 16.0 4.81

0.3333* 7326 2444 815 272 90.5 30.2 10.1

0.40 8800 3520 1408 563 225 90.1 36

0.5 11000 5500 2750 1375 688 344 172

0.6 13200 7920 4752 2851 1711 1026 616

1 2.2x10⁴ 2.2x10⁴ 2.2x10⁴ 2.2x10⁴ 2.2x10⁴ 2.2x10⁴ 2.2x10⁴

*. Density ratio (ρ/ ∆ ρ) at the critical temperature T_C for water is approximately this value of 0.33, the same value assumed by Frenkel

** Quasi-isothermal

Clearly, the isothermal hypothesis fails to yield the observed rupture pressures of around 50 -250 atmospheres for water at any assumed density ratio. The adiabatic expansion hypothesis, however, does let the pressure reach the experimentally observed low values.

What value for k are we then to adopt for pure water ? At the critical density expansion ratio of 0.333, any value of k from k = 4 to k = 6 would encompass the observed ed rupture pressures of about 250 to 50 atms. However, it may also be valuable to revisit the value of k = 7 obtained by Courant and Friedrichs (1948) who discussed the expansion and contraction of spherical blast waves in water, and fitted the experimental data to a quasi-equation of state for water under a pressure of around 3000 atm., which is pv⁷ = const or p =A ρ⁷ + B. They also derived this same value of the adiabatic exponent k = 7 theoretically as a solution to their non-linear flow equations for purely spherical ( i.e. radial) shock expansions in fluids. Their evidence that water rupture, at least in explosions, is spherical and adiabatic would also seem to be generally applicable, since all ruptures, even non- explosive ruptures, are quasi-sudden, and so, at least initially, they all could be adiabatic as well.

As to the proper value of the density ratio (ρ/ ∆ ρ) to accept, if the rupture process for water were envisaged as taking place by a transformation from its usual density of 1 by one of the usual cavitation mechanisms, such as a burst of electromagnetic or acoustic radiation into a small liquid volume ( the radiation being energetic enough to break all the liquid water bonds in that volume quasi-simultaneously), we would have a “ gas-like” liquid suddenly emerging with an expansion ratio of 0.333. Once the ‘gas-like volume has emerged, we see that it must at once expand from an initial gas-like density ρ, again taken as unity, to some smaller gas-like density ∆ ρ. by either the isothermal route p = K ((ρ/ ∆ ρ) or the adiabatic route p = K (ρ/ ∆ ρ)^k where k is now greater than unity. The density ratio must then fall from unity to some value consistent with the usual equation for pressure equilibrium, p_(max) = 2σ/r., where r is the radius of the critical bubble size.

Clearly the isothermal hypothesis cannot reach the observed low rupture pressures of 250 atmospheres or less,, while the adiabatic process can. From Table 1 we again see that a k value of 7, over the range of density expansion ratios (ρ/ ∆ ρ)^k .from 0.4 to 0.6, would more than encompass the observed range of rupture tensions of 50 to about 250 atmospheres at normal temperatures.

The proposed model would l require simultaneous radial rupture over a sufficient number of adjacent bonds, and therefore the theory of nucleation rate analysis would still appear to apply. The radial rupture might also of course be heterogeneous, and then all the various heterogeneous mechanisms of bubble formation presently considered may still be in play.

The proper value to be used for k in aqueous solutions, where the densities are different from those of pure water, would appear to be a matter for further study.

The third step: the attainment of a critical radius r_c for rupture

I must be noted that Step 2 above is based solely on the density ratio ρ/ ∆ ρ and has not specified any actual initial or final density or ( specific volume. ) However as the “gas-like’ liquid bubble expands, it eventually must physically become an ordinary vapour –filled bubble of homogeneous nucleaton theory, and the latter theory requires that, for the bubble to persist, it must meet the critical stability condition:

p_B − p_L = ∆p_max = 2 σ /R_C

Table 2 shows this final stability condition over a range of sizes , r_c

Table 2

Critical ( stable) radius r_c for various rupture pressures in water

Critical radius of bubble, r_c Rupture pressure, p_(max) = 2 σ /r

(cm) (m) (σ = 75 dynes/cm)

a) (dynes/cm²) b) atmospheres (dynes/cm² x 10^-6 )

1 cm 0.01 m 140 1.4 x10^-4

10^-1 0.001 1.4 x 10³ 1.4 x 10^-3

10^-2 10^-4 1.4 x 10⁴ 1.4 x 10^-2

10^-3 10^-5 1.4 x 10⁵ 1.4 x 10^-1

10^-4 10^-6 1.4 x 10⁶ 1.4

10^-5 10^-7 1.4 x 10⁷ 14

10^-6 10^-8 1.4 x 10⁸ 140

10^-7 10^-9 1.4 x 10⁹ 1400

10^-8 10^-10 1.4 x 10¹⁰ 14,000

Notes:

1. The ratio between the critical state liquid pressure ( 1.4 x 10⁴ atms).and the observed average rupture pressure for water ( say 150 atms) is about 100/1.

2. On the isothermal expansion hypothesis with p₁/p₂ = V₂/V₁ , the volume ratio at critical rupture must be the same i.e. about 100, .so that the radius ratio is r₂/r₁ = 100^1/3 = 4.64.

On the adiabatic expansion hypothesis ( with k =7), it becomes p₁/p₂ = (V₂/V₁ )⁷ , so thatV₂/V₁ = (p₁/p₂)^1/7 = 1.93. and r₂/r₁ = (1.93)^1/3 = 1.25

3. If a bubble is to reach the critical rupture size of 10^-8m at 140 atmospheres rupture pressure, then the initial radius size r_c for an adiabatic expansion at k = 7 would have to have been r_c = 10^-8/ 1.25 = 8 x 10^-9 m; moreover, an input of energy sufficient to bring a volume 4/3 π (8 x 10^-8)³ to the critical “gas-like” state must have been supplied to the liquid to bring about the rupture. Any initial excited volume smaller than that may indeed form a tiny gas bubble but will immediately thereafter collapse because it is below the critical size required.

4. It may be noted that incipient bubbles, smaller than those having sufficient excited volume to become critical and bring about macro rupture of the liquid, may still cause important transient rupture effects on the molecular scale. These, while never reaching the critical radius leading to macro liquid rupture, may still be of great importance on the molecular scale in locally removing a water film barrier between chemical reactant molecules in solution or suspension. This solvent film barrier phenomenon may therefore also be important in the kinetics of so-called “slow” chemical reactions in solution.

Solutions, Solids, Reaction Kinetics

In simple cases, the relationship of k to n, the number of ways the energy of the system is divided, is given by k = (n +2)/n. With k = 7, the formula would require n to be fractional at n = 1/3, and we would have to then interpret this physically as indicative of the spherical or radial expansion.

For solids, because of structural and steric hindrance, the flow orientation in a rupture flow may conceivably be only quasi- radial, and so a value of k between 4 and 6 might. then be appropriate, giving tensile strengths higher than for liquids but below the classical theoretical estimates. It t would appear that the new model may be of interest to materials science.

Again, the “slow” chemical reactions mentioned in Note 4 above, occur more often in liquid solution than in gases, and they are also the most sensitive to pressure, just as is the case with liquid rupture; furthermore, the reaction rates are slowest when water is the solvent ( Laidler, 1965). This all suggests that the phenomenon of rupture in liquid water may be important in chemical reaction kinetics. In gases, of course, adsorbed molecular films can also be present, and their removal in collision reactions would enter in the same general way as for chemical reaction rates in solution.

Finally, we may note that all the chemical and genetic reactions of life take place in the aqueous medium of the cell. Therefore, the kinetics and probabilities of the reactions of life and its evolution should be subject to the probability laws that govern the aqueous rupture barrier which must be overcome on the molecular scale if the various biochemical reactions and interactions of life are to proceed.

References

Brennen, Christopher E. (1995) Cavitation and Bubble Dynamics. Oxford Univ. Press.

Courant, R. and Friedrichs, K. O. (1948). Supersonic Flow and Shock Waves. Interscience, New York.

Frenkel, J. (1955). Kinetic Theory of Liquids. Dover, New York.

Kittell, Charles. (1968) Introduction to Solid State Physics. , 6^th. ed. John Wiley & Sons Inc., New York

Laidler, Keith, J., (1965). Chemical Kinetics. McGraw-Hill.

4.4 Chemical reactions in the aqueous environment of the Living Cell: An Entropy of Liquid Rupture

Following the above insight into the rupture of liquids we return to the living cell. It is well known that many chemical reactions especially those in solution do not take place at the theoretically predicted rates, but instead take place at rates that are much too slow [29]. For example, there are many bimolecular reactions (both in gas phase and in solution) which are too slow by factors up to 10^-9. ,so that the rate equation K = Z e ^–Ea/RT , (where Z is the collision number, E_a is the activation energy) must be written as k_a = PZ e ^–Ea/RT where P the probability factor is inserted to account for the disparity in reaction rate, and k_a is here the activation factor or rate [29].

When the collision theory is replaced by the statistical mechanics approach, the same result is obtained, but the arbitrary probability factor P is now explained as a steric hindrance factor which makes more theoretical sense. And since the logarithm of the probability is the Boltzmann definition of entropy ( d lnP = ∆S) , the rate equation then takes the form

K_rate = PZ e ^–Ea/RT, and where PZ becomes

PZ = e^∆S/R (k_bT/h)

and the entropy of activation ∆S now appears., with k_b being the Boltzmann constant.

The entropy of activation in chemical reaction kinetics can easily be related to the new

entropy of rupture ∆S_R , in the following manner:

The pressure relationships across a non-isentropic discontinuity in a compressible fluid may be expressed as

p_1/p₂ = e^-∆S/R where ∆S is the entropy change across it.

Since in any adiabatic process, we also have p₁/p₂ = (V₂/V₁)^k = (ρ₁/ ρ₂)^k , therefore we also have p₁/p₂ = (V₂/V₁)^k = (ρ₁/ ρ₂)^k = e^-∆S/R; and finally

ln(ρ₁/ ρ₂)^k) = k ln (ρ₁/ ρ₂ ) = − ∆S/R

Therefore, ∆S is proportional to k, and for spherical expansion of water, k = 7, so ∆S for this case is also proportional to 7. That is, ∆S 7.

There are three main approaches to the relationship of entropy S to probability P. First, in classical thermodynamics, as in the example above where P = e^-∆S/R , we have ln P = − ∆S/R. Here P is physically and mathematically equal to or less than unity.

The second relationship is the thermodynamic probability of Boltzmann and of statistical mechanics where the entropy S is related to the logarithm of the number of accessible thermodynamic states of the system, called the thermodynamic probability P or W, which is a number greater than unity, but which can be related to the mathematical probability by a normalization if desired. Here, ∆S = ln P ( or S = ln W). Relating this to water rupture, we then have:

(a) From classical chemical kinetic theory, ln P₁ = − ∆S₁, where P = e^−∆S and so for rupture reactions in water ln P_N = − ∆S 7 , or log₇ P = ln P / ln 7= − ∆S.

(b) From Boltzman theory, ln N = − ∆S , where N is the number of accessible states and so for reactions involving water rupture P and N are related as log ₇ P= 7^N

(c) A third entropy relationship is from information theory, where P = log_a N, with P now being the number of bits of information. Consequently, for a system composed of N assemblages of a bits of thermodynamic information, we have log_aN = P and for a = 7 this becomes log₇ P_N = 7^N.

If, finally, we make the assumption that in any time series of evolutionary rupture/ collision events (i.e. sequential assemblages each having 7 bits of thermodynamic information or entropy) the probability P of a number of accessible states is proportional to the time t available for the process, then we can put

log₇ t = log₇P and t = 7^N . When P is normalized to unity this becomes t = 7^N + const.

Therefore, since evolutionary change takes place by gene reaction in aqueous solution or suspension in the living cell, and if rupture of water film is involved in all such genetic interactions and mutations, and if water rupture involves an entropy change proportional to 7 and a probability relationship of log P log t = log7^N , then the time series of evolutionary events may also show evidence of a frequency/probability or entropy involving the factor 7^N where N is the number of collision/rupture events leading up to the emergence of the biological form.

This possibility has been investigated. In A Logarithmic Scaling of the Time Series of Cosmic Evolutionary Events to the Base Seven the results do show a 7^N factor. Therefore, this physically based numerical factor in evolutionary data would seem to merit further investigation. For convenient reference some data from the study are as follows:

Notes

1. The times of the events in years ( N_yrs) are made dimensionless as required for logarithmically analysis by dividing each time in years by the first year in the series (N_o )which is taken as being unity, i.e. as year one. Thus N/N_o is dimensionless.

5. Plot of Log ₇ Data

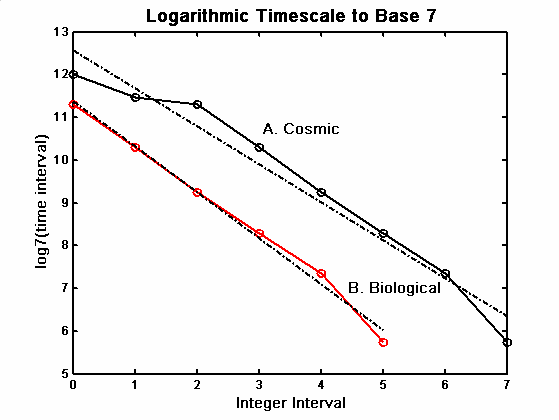
Figure 1. Logarithmic plot to base 7 of (A) all cosmic data, and (B) biological data only

For Curve A the least squares regression equation is:

(a) negative slope: y = − 0.994 x + 12.18 (b) positive slope: y = + 0.994 x + 5.22 (c) correlation coefficient: 0.998

For curve B the least squares regression equation is:

(a) negative slope: y = − 1.02 x + 11.30 (b) positive slope: y = + 1.02 x + 5.17 (c) correlation coefficient: 0.9988

This empirical evidence for the presence of a 7^N factor in emerging complexity and evolution is of course preliminary, but more examples can be found. However, considerably more effort will be needed before it can be said to be fully established and its scientific implications understood.

4.5 Entropy increase, the 2^nd Law of thermodynamics and evolution.

We have repeatedly mentioned the problem presented to all theories of evolution by the 2^nd law of thermodynamics, which states that in natural processes entropy must always increase i.e. dS = + dQ/dt. Since the emergence of biological order in the living cell represents a clear decrease in entropy, this has always been a problem to explain. Brooks and Wiley [ 1 ] have endeavored to account for this contradiction or barrier by postulating that, while total entropy does always increase, still, locally, for example in a living cell, the entropy may decreases if the necessary increase in entropy somehow gets exported to the cell ‘s exterior environment. Although this approach has not met with general acceptance, it does go directly to the heart of the problem.

We may summarize our ideas on the situation for material systems as follows:

It appears that the entropy change laws in the UF in Quadrant I of the p-v thermodynamic diagram should enter into the basic nature and direction of plant and animal evolution as follows:

(a) Tangent Gas: 1. non-isentropic processes dS = dQ/T is positive ( 2^nd law of thermodynamics holds ( “disorder seeking”)

2. isentropic stable waves : dS = 0

b) Orthogonal ( Isothermal) Gas: 1. non-isentropic processes dS = dQ/T = 0 ( “stability seeking” )

2. isentropic stable waves dS = dQ/T = 0

The detailed interaction of ordinary physical processes with the tangent gas and the isothermal gas entropy laws of the UF where the forces originate, remains to be examined.

The existence of stable waves in the UF provides for the orderly forces observed in physical processes and supplies the observed order which emerges in complexity.

The existence of a quite separate “stability seeking” entropy in the UF’s isothermal gas raises the question of whether the emergence of biological complexity might not then be essentially different in nature from emerging complexity of non-living physical systems. If this is so, then, not only the existence of orderly forces must be considered, but also the existence of an essentially different entropy system , one that is intrinsically not only affected by order but actually seeks the stability of order instead of merely tolerating it. Physical complexity would then arise from the forces of the UF acting under the 2^nd law. But living plant and animals would arise from the same orderly forces, plus the ‘stability- seeking’ flow of entropy in the isothermal UF gas. The emergence of complexity in biological systems would then have an essentially different ingredient from its emergence in non-living physical systems.

[Note: There is another entropy condition in the UF , namely that in Quadrant II (dS = − dQ/T) ; this implies very unusual properties which appear to match the human condition. This is discussed briefly in Section 5 below, and in detail in Science and the Soul/Body Problem: An Exploratory Reassessment .

It is now time to sum up this survey.

5.0 Conclusions on Biological Complexity: Do Orderly Forces Acting on Random Kinetic Motions Resuslt in the Emergence of Variety on a Probabilistic Time Scale?

We started by examining the proposition that evolution, defined as the emergence of complexity, both physical and biological, arises in chaotic or kinetic systems which, when not at equilibrium, receive an input of “stressing” energy. The only elements considered in this system are suitable material particles ( essentially molecules and gene pools) undergoing energetic, random (i.e. kinetic) motions.

Our analysis concluded that several physical elements were thereby ignored and must be included in any valid explanatory system. These include, the presence of (1) orderly forces ( which we have argued are best explained by the existence of a universal wave and force field (UF) (2) acting on random kinetic motions of molecular species in space and over time, and (3) in the case of the aqueous environment of the living cell, also involving the entropy change in the rupture of water barriers between reacting molecular assemblages, and (4) the presence of two new orders for entropy change direction governing force interactions with the UF, in addition to the long standing rule of the 2^nd law of thermodynamics for kinetic processes among molecular species.

If the orderly forces are, say, a UF wave passing through a kinetic motion field, then, because the wave is extended in space it will affect the kinetic field at one point only over a certain interval of time set by the wave speed. This will inevitably introduce further quasi-ordered variation into the kinetic field over the space of the affected field and over the elapsed time at any one point in the field. The order of the UF wave is therefore not manifested in the physical field directly, but instead appears in a space- modified and time- dependent manner at any one location. This would seem to mean the emergence of variety from the interaction of UF wave order and random physical kinetic field. The process is deterministic in that the UF imposes order, but it is probabilistic in the time sequence in which the realized ordered system emerges and in the variety of the realized order that interaction makes possible. The various physical complexity examples discussed by Nicolis and Prigogine could be re-analysed from this point of view; e.g. snowflakes emerge from a super cooled cloud under the action of an orderly vapour force field in orderly types, but they emerge individually on a probabilistic time scale and are individually highly non- uniform in their fine scale structure.

Four obvious approaches to a better understanding of this new scheme would seem to be : (1) a re-analysis of the emergence of physical complexity with the inclusion of orderly physical force fields, and (2) a detailed quantitative analysis of molecular genetic and metabolic interactions in the aqueous cell medium, (3) a theoretical analysis of the interaction of order and probability in physical systems, (4) evaluation of the implications for biology of the two new orders of entropy change now theoretically available from the UF (namely “order stability” and “order seeking”).

The suggested new approaches, if eventually validated, may not greatly affect much of current biological investigation, working theories, and progress, for example in the marvelous structural complexities being revealed by molecular biology. However, a new attention to the force fields involved in these processes should open up many new avenues for experimental exploration and verification. At the theoretical or conceptual level, it should perhaps also be noted that the interpretation of the conclusions extends well beyond the autonomy and methods of science into the other two methods of the rational investigation of reality, namely philosophy ( ontology, being ) and theology ( ultimate meaning).

In summary:

1.The neo-Darwinian proposition that biological evolution arises out of purely random physical processes alone, and then proceeds via probability laws, is untenable, since it ignores the orderly physically forces that are acting.

2. The proposition that evolution arises from a combination of kinetic disorder plus orderly forces is presently tenable for non-living physical systems, but it still does not account for the violation of the 2nd law in the emerging complexity of biological systems.

3. The proposition that the UF is the source of physical force ( wave energy exchange ), structural and flow order (entropy minimization) is tenable, and therefore the UF’s entropy change relationships must also be acting in any interaction with atomic and molecular material systems. These relationships appear now to a) agree with the 2^nd Law for the tangent gas in Quadrant I of the pressure-volume diagram, b) require zero entropy change in material interactions with the UF’s orthogonal or isothermal gas, c) require negative entropy change in interactions with the UF’s dynamic entity in Quadrant II.

4. In addition to the presence of orderly forces, there are now three entropy change regimes, instead of only the 2nd law, that must be considered in evolutionary change.

5. These new entropy orders or regimes appear to point towards an essential entropic difference between non-living and living systems in the case of the UF’s orthogonal/isothermal dynamic order in Quadrant I, where non-living physical systems obey the 2^nd Law and living systems obey the UF’s orthogonal/isothermal gas law.

6. In the case of the UF in Quadrant II, the entropy decrease law (dS = −dQ/ T) appears to point towards an essential difference between plant/animal systems on the one hand and human beings on the other. If this property of the UF is valid as interpreted here, then science may be at a frontier between itself and philosophy/ theology. Science is ordinarily thought of as being concerned with measurement and with the quantitative laws of the behaviour of matter. However, Quadrant II in the UF appears to present a dynamic, non-material substance, extrinsically rather than intrinsically quantified, and “ order seeking” in its entropy law, i.e tending towards the intellectual.

`

The new statement of entropy change appears to be theoretically valid, although it may not be directly experimentally verifiable (or falsifiable). In short : the differential equation dS = + dQ/T is a rational, mathematical, scientific, physical statement and a verified scientific law describing the direction of flow of non-biological ( the 2^nd Law of thermodynamics) . What then is the nature of the statement made by the differential equation dS = −dQ/T , both physically and metaphysically? It also is rational, mathematically sound, makes a physical statement, and describes the flow of information and order seeking, or insight, in human intellectual capabilities.

Does it also raise a question as to whether the statement constitutes a frontier between, or a bridge to, philosophy/ theology, which have rationally affirmed the reality of spirit for millennia?

It might then be tentatively restated, and rather loosely, that the new theory conceptually means that (1) the quantitative interaction of the UF with material particles (condensed from it in Quadrant I [23]) and the subsequent cosmic and biological evolution is a concern of science, (2) the interaction of the UF in Quadrant II ( soul/spirit) with matter in Quadrant I constitutes human life whose evolution is a subject of prehistory and then history, (3) the meaning of the theory is a concern of philosophy, and (4) the origin of the UF, its purpose and destiny, and the purpose and destiny of humanity are the concerns of both philosophy and religion.

7. In the mid-1950’s, Lonergan [30] critically analyzed a wide variety of scientific theories as instances of human insight ( and oversight) and of the nature of rationality or the act of human understanding which leads to the development of natural science, philosophy and theology. He then developed a philosophic world view which took into account both the classical deterministic physical laws and the statistical probabilities of experimental science in a synthesis which he termed emergent probability. It might be of interest to now see how his emergent probability alters or survives when the UF and its laws are included. The new orderly wave and force field would appear to relate to his classical deterministic laws so as to make them more concrete, while the new entropy laws would appear to introduce discontinuities which separate distinct orders of existence, and which must also fundamentally affect probabilities attached to the emergence of events.

References

1. Brooks, Daniel R., and E.O. Wiley. Evolution as Entropy. University of Chicago Press, Chicago and London, 1986.

2. Nicolis, Gregoire and Ilya Prigogine. Exploring Complexity, W. H. Freeman and Company, New York, 1989.

3. S. A. Chaplygin, On Gas Jets. Sci. Mem. Moscow Univ. Math. Phys. 21, 1 (1904).

4. H. S. Tsien, Two-Dimensional Subsonic Flow of Compressible Fluids. J. Aeron. Sci. 6, 399 (1939).

5. T. Von Karman, Compressibility Effects in Aerodynamics. J. Aeron. Sci. 8, 337 (1941).

6. A. H. Shapiro, The Dynamics and Thermodynamics of Compressible Fluid Flow. 2 Vols.( John Wiley & Sons, New York, 1953).

7. R. Courant and K. O. Friedrichs, Supersonic Flow and Shock Waves. (Interscience , New York, 1948).

8. Horace Lamb, Hydrodynamics. 6^th ed . ( Dover Reprint, Dover Publications Inc. New York, 1936 ).

9. N. A. Bachall, J.P. Ostriker, S Perlmutter and P.J. Steinhardt. The Cosmic Triangle: Revealing the State of the Universe. Science, 284, 1481 (1999).

10. A. Kamenshchick, U. Moschella and V. Pasquier, An alternative to quintessence. Phys Lett. B 511, 265 (2001).

11. N. Bilic, G.B. Tupper and R.D.Viollier, Unification of Dark Matter and Dark Energy: The Inhomogeneous Chaplygin Gas. Astrophysics, astro-ph/0111325 ( 2002).

12. Power, Bernard A., Much of the work leading up to the present theory has appeared in connection with studies into the scientific basis for the image formation on the Holy Shroud of Turin. Some of these are as follows:

13. ---------------, Il Meccanismo di Formazione dell’Immagine dela Sindon di Torino, Collegamento pro Sindone, Mgggio-Giugno, pp. 13-28, 1997, Roma.

14.---------------, Caratterizzazione di una Lunghezza d’Onda per la Radiazione che Potrebe aver Creato I’Immagine Della Sindone di Torino. Collegamento pro Sindone, Roma. Novembre-Decembre, pp. 26-36, 1999.

15.---------------, An Unexpected Consequence of Radiation Theories of Image formation for the Shroud of Turin. Proc. Worldwide Congress Sindone 2000, Orvieto, Italy, Aug. 27-29, 2000.

16.---------------, Image Formation on the Holy Shroud of Turin by Attenuation of Radiation in Air. Collegamento pro Sindone website (www.shroud.it/) March 2002.

17.---------------, How Microwave Radiation Could Have Formed the Observed Images on The Holy Shroud of Turin. Collegamento [ro Sindone Website, Jan. 2003. (www.shroud.it/)

18. --------------, Shock Waves in a Photon Gas. Contr. Paper No. 203, American Association for the Advancement of Science, Ann. Meeting, Toronto, Jan. 1981.

19.---------------. Unification of Forces and Particle Production at an Oblique Radiation Shock Front. Contr. Paper N0. 462. American Association for the Advancement of Science, Ann. Meeting, Washington, D.C., Jan 1982.

20.---------------, Baryon Mass-ratios and Degrees of Freedom in a Compressible Radiation Flow. Contr. Paper No. 505. American Association for the Advancement of Science, Annual Meeting, Detroit, May 1983.

21.---------------, Summary of a Universal Physics. Monograph (Private distribution) pp 92. Tempress, Dorval, Quebec, 1992.

22. ……………, Properties of a Universal Wave Field (UF). http://www.shroudscience.info/ November, 2005.

23. ……………, Cosmology of a Binary Universe, Part 1: The Origin, Properties and Thermodynamic Evolution of a Universal Wave and Force Field. http://www.shroudscience.info/. April 2007.

24. L. W. Gold and B. A. Power. Dependence of the forms of natural snow crystals on meteorological conditions. J. Meteorology S9, 447 (1952).

25. Nakaya, Ukichiro. Snow Crystals: Natural and Artificial. Harvard University Press, Cambridge, Mass. 1954.

26. B. A. Power and R.F. Power. Some Amino Acids as Ice Nucleators. Nature, Vol. 184, 1170. 1962.

27. ------------------------------------- Vanillin, cis- Terpin and cis- Terpin Hydrate as Ice Nucleators. Science. Vol. 148, 1088, 21 May, 1965.

28. Brennen, Christopher, E. Cavitation and Bubble Dynamics. Oxford Univ. Press. 1995.

29. Laidler, Keith, J., Chemical Kinetics. McGraw-Hill. 1965.

30. Lonergan, Bernard , S.J., Insight: A Study of Human Understanding. Philosophical Library, New York. 1956.

Copyright January 2008 Bernard A Power..\index.htm

Back to Main Page